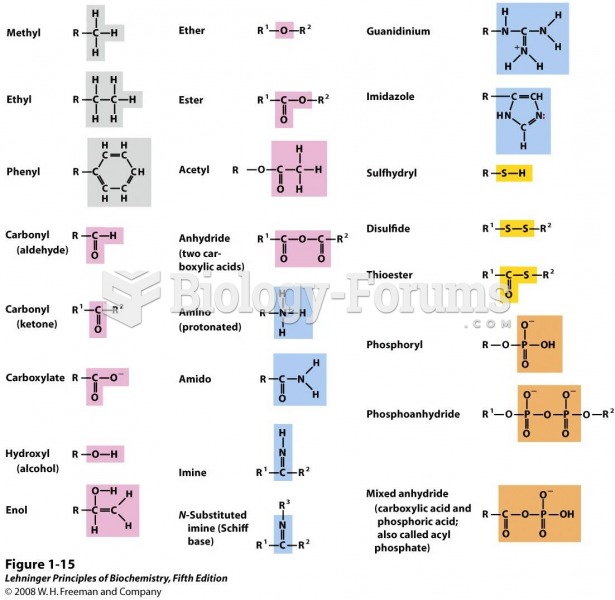
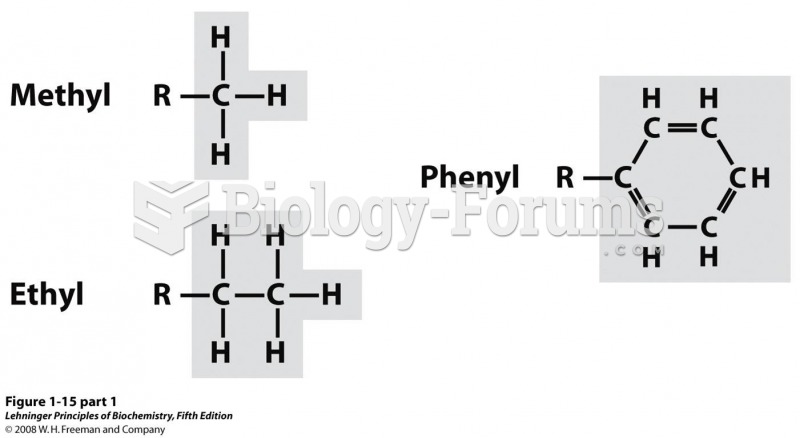
Assign priorities to the groups in each set.
(a) -CH2OH and -CH2CH2OH
(b) -CH2OH and -C(CH3)3
Question 2Each molecule has one chiral center. Draw stereorepresentatio ns for the enantiomers of each.
Each part has a tetrahedral chiral center. The chiral centers are labeled with an asterisk.

 Question 3
Question 3Following is the structural formula and a ball-and-stick model of cholic acid, a component of human bile whose function is to aid in the absorption and digestion of dietary fats.
 Question 4
Question 4faqp7x6SDfGtcJnnrrtttvSndhtVip7sYzGeSBkIGU+aTRBGyAw5zzzhB0m3J4CoKLgqRPayCr9kksuCf/4xz9qVoeZRCJBgClmcMcAMcPY86pdYsK3AfLxxx+fghUgzUa0RUVZYPXQQw9NQYU9C23TwzR03HHHpVn/swkNbYpqFwCbOLdSADFJC+tl/NZnbSqtfCWQDcQBSJjMeoL9OffccyvuZF7v2Hq/M61WY08rHatsUXOsbVdsPm7nA3tKag9ZzGVeb2dfzN9X6QOU10jm89ghl4arwlJhn8EPhjeX2Dgs/eap4YQbjwjddHJHAAAgAElEQVRrfX+B0AnIcfzLV4fjDnwwfLrrj41/3gtPjUvCwpl7aOvb8S+Hq487MDz4WQXDe0+NC0nHVLCt2unzFzdJWN0yW2y88caTmZUwQrIe27XcBBAHakyAjUqb2dLBthF/Oul3acbmVvmG9EQj2ktPlmQMBMYDu5P3h5E9GPDBONgOI4otMZj6sEAmonYIHyy7r5vwAVdtyU+pqPDfcr/AnT+C/bnqqqvC/vvvn5o58+fSnwClVorNWpnaACztYbfxvAA/O+20U3p/gE4lAdawWEy4N954Y5oVu1I5ma2Zem1QDcC3Wmy5wTdLVu4ioo85ppYwcwF+5513XmqKxNRi/TCQzLh2avc8W4BoHybedkonzOPtvP8a1/4gPHDRw+GLq/QPw59/Prz4/mJhi3VCuOm3l4TnxtU4rAd/mm7ZfcIV9zyUOjlydHzo1pPCerP068Ea1LnUdMuGfa6457P6PXRrOGm9WUIH1bDODZQ/d5cGbLJrhc5ksckmm0wGflzzq1/9arjppptSXwnmkyiPPvpooW0GYvnsK1OMjUHtAdabGCD3wPxgI1MTCFaHGRAYtNUMfxqboZr0+cpEsBjvPZrB4ueefuXzom4E8OFHxcxZVGz1seKKK05WnJMznZhY8/erIAYiDxInO0ETH7A59MuRF2j405/+lLIaTgWQ2dyaozBnX2xdrY1Z7YAOBAE4fGtszeFe/HHct60G/zYbph5wwAFN1Lb+IQBaIz49ylYDda4G/LivG264IfW547wOMNEHQOR5xp5ZfNCN7UuAynY66ZcAqEo/mfD6jeFvr28Vfrnb9mH77f3tHA48eocw/yN/CGc+8tneVlUOL78uNTDVasDO4p4JE7HJDetglWqgKyJWyehxESUmw2oi6oa/iJXim2++mToDo8+b3UvOccxEzAqV9gCrVo9O+X6llVYKN998cxrtRG90YuJlIqN75oVKztnaqWjbdNe92qMMg8WUh6nC+pns64lJ1d5he++99xRFARGslok1K44Bru0x1mqhX+cG4IF3/V8/9ed7TBdwV4kdytdl6623Tvdpcw8AIlYTaAPssF42Wq103/nzNPuZnxRWRp+qJyL5tCE2r5rsuOOOqS+foAP+T5Gl84rtveaaa9Jz0J2939yb6DILIPu/tUNKAFRB6xPffzycu/+vw41vvx5eeGf8pyUmjglvjJg1zJm8HE7b++hw/asdQgNVqH/5VamB7tCAQZkzMZ8OZig+O2jxyy67LPUzsZmjHb7rCfOBCbyIH49JwATOfMWvBQBqxHySrYv6m2SEsLebes/Wq9H3/KMAThtoHnPMMWl71DIJtpsBcn/qd/nll6fMjCgwk6JNQ2uBIL/tu+++Yf755099fvJ6wsiceOKJwcRrcgZ8RF5hKQAVE3x3iOtiLoBz9wGI6luYKtesxEhVqweGhFmTX5QIM5v02myV/xv/me4UKRYsQvjfAXPVBGO60UYbpYzXvPPOW7HYCy+8kLKTwI+FBr0APBgx7OQbb7yRgiLPsQ28/WGCMF3azoLKONLTUvoAVdB4/9lXCjtf/GKYLNtB/1nCkpsdGwYnn9nXKxzagq8mhjHDHgmPvDQmTHS2fv3DtDPOET6/9LJh0dnL5mqBgstTNKEBAzzgQ0TdZCdcPiZMAnx2DHYmCL4Z1YR/j1VfEeHkalXMb8IEKhpq+PDhFf0+Kp3PJKr822+/Hd566610xR5DxCuVnxq/A4BqTXA9dc/aUYSaCC4Tn8nXhG+HeJF6WQEIOD0zWfKT0acqCT8akVnKipQy+QJEzFPNMoWVrlPtO0CrkZw+1c7j+1ab7GpdK/4GyHmuttpqqxSQ8N9heqNv/kGnn356atrDwsU8WvHY7CuGh5ky3sM999yThrwz0WK0AFOgx/WOPPLItA8AjvrCkksumbbVdtttl/pFWaD0lJQMUE9puvB1+oeZ5v986H/bHmG99XYL1zz/enjp0UHhsA2XCKv87KLwYko8zRhWHPhMGPfUQWGZbDbBubYIN44eGQZt0nMdqNptzbjiwPDMuKfCQZNXMGxx4+gwctAmof01rFbz8vtKGkDvSyBosMyCn2xZq1nRLQZDg2c1kU+liInA8QZSEyRHYA6VJk5RYDEaBSNUKSoHYON0K+8MxonZy2SrPMdq/kB8aLojwVy1+27X953AAGXvHQuALcEsmGiXXXbZwBxkgjQ5YlGAVGYlfk/1JkS5gkyk+oFIIyA5RsFlr1u+r6wBPmTC2wEYDI7n2983vvGNVPf8k6LzeaUzWGQAs4AT8ezddddd6TOKZcLgRVP366+/npbxTDOJesWYyQ+kLL+onpQSAPWktgteq/+MC4TlVlsqzDLD58Pam/8gbLvbkeHP5+wYxpx3eDjriSkzixY8bVms1EBTGjDAGZiOOOKIquAnnhgIkpjOyrGaoNEbSc7HfyVGMDG9WTHySRAl4zr5JIEAFodUvhhMJAZ4YbgGWw6mVqHrrLNOOmgb9AG7vDgH0McZWxSLCZWJjx6KJsPLn7OnPzMJAX9A4+DBg1PQSfcmKpE4zZoSW3UfdMofRF/ACKov0VbaXNs2wq5gfCr5QLWqvlPzeSRaxOB6PgAY/R9rw1fPM11LgE59iT8UsfDg5wfARh+t6OgcQVL2fLGMVAna3HjTU1ICoJ7SdBevM+HDD8K4/rOGOWaapotnKg8vNdCYBp588snUx4d5q4hwcgVAqgk/Is6wMhwXEaHyokui8H1hSrHqtHIEiqLIecNpGmtgcsVI2S6D/Oc//wm77bZb+hmIkkuGAze2ATMUBTMhgzQfD4yESUH+IdfFXGCPmPE6WUTLuTc+NNpNyLjVNyAk+oYzKx1hWNotgJD6MJfwh2HCagT4tLv+U9v1MTLYmKLiOc6WB4g8Z4cffngKSJnIo4kTqCJ+EymXLYMR8hw6vqekBEA9pelmrjN2aLjg8L3Dbj/ZJKz9g1vCumdeGvZaboZmzlQeU2qgaQ2w1Yu4qeaHkT8xp2VhyNFMlf8duOAAXYTuNkEbNOVeiQKwmCCtOplTsk6nGA+giBmFGU4SPf4/xErTdeNnbAiGh3nNOfmNMKWg/pnHhPNiJqyO/QlZ5rApY7XBWjRcJ4rVNtBjRc9fi2+MvdNE5piIhNADdswaTB58bEopNdCsBgBpjBHWhxgnPC+eH87c0USNiWXmJJ5bz3C2jOP00RIApSoq/4UZlgk/OeqP4Y8nnxiO3nWhcPNBe4ST7n+/VEypgR7VANNCUbZGxQAfg1kWmOQrLKMu/xxgIivob/4DkvnFxHcm7GjawPDY/JRghu68886U6eHXg+HgywCoWHUCQPxLRNUQgAcAyn7mZGszSP5BTEX8jFyvlsOn6BVgScK7nqTr05uo80+0Dcdg+WqswrUDB+g48QB4THiA3ZlnnpmuwkVN+b6UUgPNaMD4YKEBbBOfmcH0Oayp/pbtd/EasV/GMhYUwBIQ1FNSMkA9pekuXGeGeZcPm+03MPxoxjvD7/9wXyghUBeUWR7asAbkzOFzkzUT1ToJ1kZUmMm3mjDPMCehwAEKzM0ZZ5yRAhYAh8mGjw8HXmwMkxXnVowFp8zrrrsuNZWIFgKmvJr05VMxAMsNY/Up5BogIL7D3GQ/KyOCyHdAAX8fkTD1hBkP+AHAOknkArKyloSukmSdT/0uTNnWIxihUkoNNKsBUZ8RRHuGhMVnJd/vsr/F985hr7CeBEBTZVy1lWcnR3dYzUaHv9j4U7wmE0PWFWzimNfDyx+EMN8XF
Question 5wjdbQSD2GtNXlPUtfxiqtYA50aOqRgXuVvqSdy406QKsFTLZ+J7q0abWGIrUOgclH0fGR/X8qzww+HQzLQm7Dk6U3rWTfb+gCU5coj3fH74/8QkgL4DgLKfYxmOnvyW+C8V8T/xfGCA+DKpcyeI3CuAI0dSbBgdxfDjyFQBnJzUReZky3BYVTZG63TC/ZR16D0awJgCMBhVJm7+PZzbmcNJtt/FuQVDFPulMp47YDz+3hN3P81vIjfaE1frxmvwUzBocsayUnVbaO0NNthgssG0G6tQ99QGexPCfffdlyaGQvWzi04esjkxjH7u1nDBn84I1z72anhv9Ijw5L8uDWecfHF4c41Dw5+P2iwsMmP1lXXdStQoYABFRxogUZoydQKS7Lu10rrXOGX501SiAT5ATEVrrbXWpEGt0q0xa2FahDULmfccYmtQ2wbD/OrOik+fw+AwxUhQmB8AfQbCRGxhhTgkb7PNNlM81zbbZPLSV03oTF38fpjNiO9M8NnPsYz68Z2R66hIgkbnY2669957u2Wn7kq6rfcdx2xZfZm26AwTpr2MMRyfORiLmAMwfZ8tA2TST9F9oerVpfy9b2nAQkSf8rx7hoEZZmnmaL5+GORsv9MnY7/07MmgLehAYENPzjW92gTGmRFbAXVy7oMyiTTrQAZand3fCrOdYtUqGsNKccSIEWkHsQID2Dhf+i0OyiH0D7Mu9Y2w50WvhiR5J/zrtOPDb0/5S7jq7sfC3efvFVabvfVNBoVLTW71zAyx++67p9S+AdRqkg6tdNUdqCyl72nANgwYEtsLiLISKpsViw6DGN8YkVcmW9FUcvZwyGVq4pxsQYJJiv1If+MLANBUyy8UrwMsASiyT6PU8yK3UNbBuYgPUCzjOOcH9ouKsjHxW9FjurMcBieuqCWOtIcas170wTA5+YtJEbNlvAfoiooxTZQdk5s9omJ7Fj2+LDf1aUBqCYsdcwmfQf1MH5QdPtvvMMPZfgm4S7RoIcR5uiel9bNpD9UeJQ5poswgSxR9tO2rgtBYA+XZZ5+dAgyTu8G4JwWl7/rqJ9LC6pijlwHJ4Ok7qf5NGCh4A0ocwHqqniYp4cCof4hctIjcD1aDBK3JR4N+TXDAkNU6MBS9/nuqruV12qsB6fBFQQFAzEk777xz6mMjygjtrV/oy5H2xjBgFJiumJ385jkUneTZBaawNgBSUSCB4VUPky7Wwt8dd9yRmtAkO4y5SJi29FfO1AZmEsPgs59jGQOvOuX3laqlcWWjKa5WuZ76zaqbAzrTlqzXdJP1vcB+RRNXvoxtCzBHWF8TGIBTTaQgwAi6f6DVlihSAzhHKX1bA0zO5lmA2nhgjrO4x8QS/Y7EfvnTn/40XfxYOFl497T0S3p6xu3CHXqo0fBSawM+0ndzuJTIzOqtmhgIoE4IE00n4VJskGrHdPV7g63cFoCOqBLOmAZvdTHYq+9nrE9IkbMO4Hs0oHp2p1ixmYjQjih/q3I0eTURmmiCEPJopSltOeSOXRNKXErf0gBKmwMwEynwIExd5FURYWo1iUb2h19R1uen3jk8Q5hJQIbjpYEWeGci0x85MXPcBn74C3ll0mUec4xVafzsN4AOM2UQBgAsSqIvUbW6MLk7B2dPTp+dIHwu7HIPCGHEARQglT8G36e487dFmT8stDLGKWy5sdWzDagySxhnpQRgxhAdhxFmfgT6nDM7Rlk4cUAHRnvjRrOd0H5TUx3MzeY7zyWzLFOxZ9xcrU/+/e9/T0G659EiqF1zSMcDIAOllQn/AIOs/AFCXdG1Bl/AxkBaREzikmxBpV7RbrVCdYucM1/GvkMa2ICArhfBAg1H4cNg9UTUPzIt8XemAuYDg7nN4eKKLf7e1VcrRPct6RiThGy3dFpEOFjyY5JjxWTC5ABIxXBkbSQtfSmlBopogOmX3w1Gp4gAPhYWosD47gAeTDAYKLl8MJL6tIlY3/S8A2mAPhOXY4AEv8fPBmDAwPMKVGGqPHci1KrR8cABCh8o8Hx3krgfvoXGDbrFigFrwE58zo0vTBKxjJ24mSmMq1g7YwR9yKRNDwChhZnVPcbn/9u7FrCqqrT9AgoIIuIV856OKGpeJu+Zd1MzGytHyWc0NVNBsxqzmmzsZjhjNtaTjmXmbxqlFahpav/kJUnKSxcvYf1eBskLIgqCCIfDWf/zLtx4QA6dI4fDOfB9zwNnn33WXpd377X2t74rJdoljZv1ElcykkJVFwHOD2oKKGig5oDEucn3Lp9J2rzSFpCZ4J39fnMUdbdUgREoLlIEkrsOTlDu2jg5ucOj5ISLFXec9jI/BIagf/bZZ1pEx0WCUiBjV+QocMXLs0/cPdKmh0wVVUvsozXzw2toc2CQETfB+M5PjpMLNRcZ7kLJVHDH7AwiM0nVBZksugzzRWIsivbUT5UFJW+8loJDesHQ9mPOnDnaRogvHS62fDmQ6xcSBEpDgC9LSivsJT5zlPZQykGmiZ+0NaDNHzdCfL6ZPJVznPOMkh2q49gOifPdOhAiv1PaQSkS01zQk4WLNl3uqZajNKO4gJwqbK5NnJvcubob0Q6SasDIyEiNLec3MWbAOYO4KycDRPU211caq8+ePVuvryxDZoc7coYHoHqLmxxufmhWQIaqa9euRlVFPqnuJIMpVLURoB0QpT/WJil8J1KAweeO2hBKHSua+eFdcj4DlJ+G79Ysw4cHLxdkM7/+LOSe3ITl736BJMN20pKJxNiFmBlxP+4dNQ6RC9bjcEZBLhhyiFzMqDriZCUTQNErxWZc9LhzNDjLW3nUKLpmoCYukMxvRP01GaJbIS6QtN2hDQ93m0zeyMXGljrAmgGi8XZJxIeHTAbF69yRkpsuacdV0rUlnaO9FMXZ3ClTPUApla04ISVdX/wcbYSIP207iB8ZVT7sffr00QwSxepchC2ZiYhdOBMR99+LUeMisWD9YVy/xdwTIO27NVj24UFcLrjtBc3knsSm5e/ii8IHpXjr8r2yIOCI2otj5iJquNXzRcsNBJkbMjKUDvFZ5AJLlQ2lF5R6UK3DDQWJ88gIhMh5S3E81wB6qdBgk14rnMdkoKi6njBhAmj8Tfs4ekaSmeAconif85GSaarvGECRubWsVdoVdY/IGFLyTFstY+PEsREXknVAOjJJXFu53jIMgS2ilJqSXY6ZLzFbayXPc20VqtoI0KyCKld77foqFC3aADmVrv2k/v6H6io8OlHlWlWcFjdMBQaPVlsuK6XM59WWqDaqenB3NXXhSrX2/UVqxl0hqnrLKeqzM3n6qokTJyovLy917NgxlZmZqWrXrq2aNWum8vPzrWot+6HZbFYLFixQNWvWVL1791bJycl2V7pnzx7VvHlz1bhxY7V582a7rps+fTrD++i/F1980a5r9u/fr1q1aqVCQ0PVxo0b7bqGhYhbRESECggIUJMmTVK5udZ3xO5qbBZMSkrS9ygoKEhlZWWpvXv36nGNGDFCmc9vUVFtqqvg7lPVwpVr1fuLZqi7QqqrllM+UwW3+Jr66e9/UNXDo1WidbfS4tSwwGA1Wj8oNpuWHyoBAnPmzFE9e/ZUnAf2/k2ePFmFhISotWvXKpPJdBMK+/btU23atFHh4eGqadOmys/PT82cOVP/DRkyRD+f/H7bbbepunXrqtjY2Jvq+Prrr1WfPn102V69eqkXXnhBLVu2TG3btk1duXJFRUZG6vVo7Nix6rXXXlOvvvqqGjlypK7v+eefV1xTKpIsFot6+umnVVhYmFq9erVin7jmkO677z593K1bN439Qw89VCKOtvp/9uxZPc64uLgiRbZu3arPnzp1qsh5+VK1EOB7oEaNGqr48+GuKBTMCmf2zg4GKH3nFBXq1UrN2XvlRstZ+9W8tt4qJGKzSstX6vLly4ov1i5duihO6C1btmhm4+rVqzeuceIR23v44Yc1I/SXv/xFldbOmTNn9AJZq1YttXjxYod60b9/f70AcUEaN26cQ9euWbNG1alTR3Xo0EEdOnTI5rXE6+WXX1aBgYGK7aWkpNgsW5Yf2E7fvn31y4GLfqdOnXSbmZm/qZ1TQpVXqzmq6C2ep9p6h6iIz
Question 6WkqXwkDVBbsK8O1R48e1fNt3rx5djFAUVFR+vnnxqM04vPesWNHtWTJEs3gcA5w88D1pF69enpOcCNR2maKzzY3NayHGzGuCT///LMaPHiwIuNz7ty5m7pw4sQJNWDAAF3WHZigmJgYzQRxHRgzZoyaOnWqGjp0qMaga9euatWqVSovr2DDedNgSjnBDVmTJk00A8U6ySwS3/j4+FKukp+qAgLr1q3Tczo7O9sjhut8FdjvyrMycWBlHFK7zEZkNyv9f2AXTH2qOzI3rUB8BrS3EUXMzGpMcS7tSijyLm40/LvN2VmA3k2Mc0IRMd3naUxJewKK1g2iSJkiY+r/jRxDtNlxhOxRgdmqj55XdCOkWzrVTRRL0zPOmqirp+iftlI0GKWNgy11nPV1t3JMmywaSVLNQK8SqhXpVlxTHcPKuFR0mR2Jord4Kp7qnolNK+IlncetAF7JrqG3EN3nbamCiw+XdnW0W2HYhtKIzztzjNGwlyobzgHOGxpFU2XG70y3UZoKjs825xnVYvQko3qH6neq27hO0COyOFGVTvsH2slQHVeRxP4zthLXG46Bjgtctxigkp6zNHKmCzLtfRwleoHRJIFjpN0PVYBU1XNNEqraCFD9xTnnymCGZUHc8affrtYUriYdRPzuFPhcL5+VeAl5aAzkp+HYkXTUvbMz6hdp3Qd1O3ZHw2vbceS8CaNCfPUEpscSJxvp9wKl2dW13ylEHTaZINrxUPdPI2nmGuJCsmDBAu0Cyv7cClPB2BrWwca48JPBKm0hLt5dYkDjSxqS0S6BOZXGjRunjcrInJEhovE17QBcQbRXItFmgm6xzz33HPKTluFIel3c2bk+it7iuujYvSGubT+C86YCbzF1NQkH43cj5caDgkt54JMiVAUQoFF9VFSUNlYuzSCa9jV8adMO0B6ioS69LRmbpiz2bpybNI6mUTBf/GT0S/Mc5QaN9kC0NeJmgI4BFU1kMvnnTCLjRC8eIUHAQIBzlOEUuGHwFCryfnJep804vSEac/f7F1aZf/koTIoMUC6umrzgG+R3kwW2T40g+CEP2bkFUhfuYijFMF6yhZW54IASJ7qsM3ghF2j2gTtHLmy3SsV3unxguFs0Asc5Ui+lPFzc+VIg48MXAw2c6Q3jCEPlSJullaUkjEbrvGf5uVdh8vJFkF9xAaMPagT5AXnZ4C3mr+bTGxA9dz8Kn5T8yzhqUsIAlQZ2JfqNzDulvJTY8Dm2xTDQ25CbEyPQoT0QMLYPPR3LwgAZ7dBYmv0rjUkzytLTklIqRk9nSAwhQaAqIEChAdd/T2KMy4kBqo52sz/F3mfbwvf6nb+0YTiaPUIfy2CE1vbClWRKhIpS3qVkpCMYjWoXSBX4a0UwP0av2Da9PMhYOEP1Zq3+MtogU3QrDJBxPRkyLvKUwDijj0a9t/Jp3KtqwaGo7XUFyRTlFKE8XEpOB4Ibgbf4Cu9vu9n4dO+zaHvjQcFw/aAUuVC+VGIEKNFkTCx6UzK2DtUqdM82KC8vT6uljefLOP97nyzPep1BR44c0ZIge+tizBwGixQSBCojAnzfMAQNBRTctFAlzPRTFBx4ivqL96X4Fr3875V3CLoMuR2ZezfhcJZ1c9k4tmUXLjUegO4NDH2I9e8Vd+wsxqIkBqikc46OlFy3s/roaNsllfcO6YIht2di76bDKHqLj2HLrktoPKA73OwWlzQMOeciBPj8MoM8432R2aHKmdHQ6Y5OKQrj/ND+jok8+bu9RJshBkh0BjE4oCMMGMs60ldn9FHqEATKGwGacdDmk+EiOEdpO8v4UAxKStMRRgin0MBT0iS5ngGCH9pNehb3ZK7EE69/i3St7bIg88CbmL00Ff3mzkCngjRU5X0vXV5/ScxOSedc3jFnN+jXDpOevQeZK5/A69+mF8SDsmTiwJuzsTS1H+bO6IRKeoudjWSVqY9MEJMFM34PJSeMNUUVNO1oqCJjBFkaTZMpsodoa0eRPA2BnUFkpOgcYS+xLF8SQoJAZUGATgS08+RGhNIexpci88NgpFT5MpI443QxsCZV257ABFUAAwRUaz4BH2x8FrWW9kWLdj3Rv1c4mvdaBK/HY/HxjNaFarPK8uAY4yhuA8TzJZ0zynvuZzU0n/ABNj5bC0v7tkC7nv3RK7w5ei3ywuOxH2NGa0Pf5bkjlJ6XHwLMSTdmzBidkoH2O/ReIjEAKtMtGIENbfWAjgX0TGLQQlvpLGxda+s87X9oAG3tFWqrLJMdM6I0jaeFBIHKgACD3XKDwmCgjPLPOcnnnPk1GWSTzBDV1swWwGMmy2a6qeKR1N0Ni4rNBWZKxdFv9+H4lUDc3q0XOja8ofd3N6DK2h8+CIy8ajKZdPoI7lDpVsvotO4YUr+s4zWuN6Uexbf7juNK4O3o1qsjKvEtNoYsn05CgGpdMjuGepdziF6G9DRhpPiSQulT7UTvSO5GWY7pb5xBbJuLP9O/cB6XRvRsY/R1ugQLCQKVAQFKZJlmhY43DCFBYmgJekYygS6ZINqjMgI01WB0QOBvVF+7dX5Ij4hWJJ0UBASBKocAI8oWD0jKAIWMvBwcHKwYLf7LL7/UQUETEhJ0xOZGjRrpaMeMSOts+uWXX3QAwBUrVujgrMXrZ2DF+fPn6yjU5RV8tHib8l0QKG8EGNSzRYsWOugvn2tGbWcgX0ZTZ2Rwg/jb559/rgPvGmUYcNOdqWIlQJWBNbZnDMyPFrMOx8MjEPHHkELLc+ZHW/Wfahj+yAg0F62QPUhKmSqEQHEJkPXQGdCQ8Xa4I2WyTnqiMFbP9OnTdUJi67LOPGYwVgZ6o2SJ4TGYK4xqMdpEMAs63eQZDJFhKoQEgcqAAG3pKFVlyBYSkwRTzcVnneeZ8Ns4xzAsRhkG3KRDA+dMSdJaXbCC/wkD5IobkHMI8++4E59OPoQfbgoNUAPr/xuLEbVd0RFpQxDwHARKY4AqchQ07ty6datOWExDbcbdCgsL08wX3d9p0C0kCFQWBAz1l7U9DwPu7tu3Tw+RibbpEk81WPEyAwYM0IF5aT/kjlROcYDccfIgqwMAAA2CSURBVKjSJ0FAEBAEyo4AI0FTCsQ/IUGgsiPAgL2U8tDmh0TJD5kf2vuQaPPDc5TyFC/DUBT0HnNXqhAvMHcFQ/olCAgCgoAgIAgIAjcQYAgIMjs0ajbSwdz4teCIqjCGqihehtJQ5s9zVxIJkMvuTCn50VzWB2lIEBAEBAFBQBCwH4FBgwbhlVdeQUpKir6I7u9Ue1HyQ+IxJUT8o0cYiWVoB0dbOdrJuSsJA+SyO1NKfjSX9UEaEgQEAUFAEBAE7EeAOfg6dOiAPn364I477kD//v11MnB+MjYW81HymHY+tAMi8TvzU06ZMqUwjIX9LbqupDBALsO6lPxoLuuDNCQICAKCgCAgCDiGABNdMwUGA5GSGSIZgRCNOEDt2rXTsYAoEeK5lStXFhpKO9aa60qLDZDrsJaWBAFBQBAQBAQBj0Pg/vvv13ZA9957L+gBZhANpA0yDKPXrVuHYcOGaelQq1atjJ/d8lMkQG55W6RTgoAgIAgIAoKA+yDwzjvv6GjQTINBzy7a+MyZM0fnBmP8HzJAZJQYMfqtt97Cgw8+6D6dt9ETkQDZAEZOCwKCgCAgCAgCgsANBGgM/dVXX2lGh0zQ0qVLdQLj1q1bg8bSbdq0wY8//ogJEybcuMiNjyQQohvfHOmaIFCVEXDXQIhV+Z7I2AUBA4G0tDTMnj1bf2Wi4vDwcLc2eDb6bf0pEiBrNCrbsfkSju2OQ8yaddi85zDOZl5AYmIKLiTuwIadp2Gyc7z5mSew5+P3sflkrr7CfH43Vn90AJctdlbgQDHbdZtw4dB2xO0+Y3e/HWhWigoCgoAgIAg4gEDdunV1CpouXbro+D9G0mIHqqjwosIAVfgtKI8OWHA5YRFGd+6Hv+3MRsM/tEBAciyiOjbBgFc3IOZvEXjsnV9wzZ6mLVdx+sBGLJgxB2tP5OgrcpO+wrpP4nHWXg7Knnaul7FVt/n8XrwfeT8eW3sKeQ7UJ0U9CwGK1f/1r3/pjNO5ubk6k/STTz6JS5cuedZApLeCQ
Question 7BVAgPM1ODjYY0cqDJDH3jrbHTcnf4RJI19BemQcPn5xPAb17IGBD8/Hx1v/id6BjdG7Ryjszr3qHYiWvQbij/WrFzYY2ONlfBH7BNr7F55y2oGtuquFdkf/zvXg6yOPrNPAdqOK8vLyMHPmTDRt2lQnFh0/fjyYhJHh9ZcsWQJ6kzz66KOw9jpxo+5LVwSBKolARkaGRzNA4gVW6R7bXBxb9So2mgdj07jWRRgdv7BJWDDlAvJ2Asp8FtsXTMaHCSbcOWsRnrunEfgwmM/uwIrVB3A17wJ+8+mNmU8+gNbWPIflKpK+icXarVcwcl4UOgXkIyX+A3z0fRauJSch8L65iLq7AXyscTWfwba3/we/BIYg4/9y0e/px9Gvvg/yU+LxwUffI+taMpIC78PcGX/EtW+t6wbyL8Tj/Q++R75/Do4dyoIl3LpiOa4MCJjNZpDhSUpKwuTJkzUTRHdbRpb19/dH+/btMW3aNNDOYMSIEdi+fTv8/Pwqw9BlDIKARyPg6QyQ9avNo2+EdN5AIAuJu04AjbuhdU3j3PVP72C069EcvshHxrEf4PPQYrw19iKWPL4UR6jdytiNJ4fNx7UHnsCceXMx8Odp6DYuBmfyrepRFlgyvsa/392pVWBZ372EqTF1EBE1C9P7JyN6yuv44UZoCH1h+pezMHF1Tdw3+REMzVmOJ1b+ClPWd3hpagzqRERh1vT+SI6egte/zypSN67uwwujFyD/gUhMj3wEdwWZUQ5mR1aDk8OKQIDMTXp6OoYMGaKlPYsXL9ZB1vbv368/yfSEhoZi7dq1SE1NRe/evYtkna6IPkubgkBVRoDqabq6cz5GR0cjJibGI+ekMECV8Sn2AqAsUMrW4LwQ0GowBoaFoGHHO1Ev6xQu5gLpu/+J1Rm90a+5L+DdAINnPQz/z1/HZmsOyCcIt7VojCAt4knHrkXrUH14PzT0AULujcF/D7+GOwOKtlt70HIkbBoL0+6N2JV0BWlJl5C6axHWVR+OfgUXIua/h/Faj4ZWdQPpe/6BFZnDMax5NcC7Jpq0rK2lVEVrl2+ejMDhw4exdetWxMXFoXr1G2pWjokut0zCyE9StWrV8MADD2g3W7riCgkCgoDrEcjPz9fzkLnA3njjDUyfPh0LFy7EM8884/rOlLFFYYDKCKD7XV4T4QPbAEl7cMgeNy0vL3ihgFMyZaUhy5QD83Uxi3+zDmjolYXLOTY4KUs2zp++gEsZOdclMz7w879Zq2pOS8DSJ+ZjT51BGBxeCz6w4Nr507hwKQM519vy8fO/ibm5dvYE0nLNsNho3v2wlx45isDbb7+Nc+fOaXUXr1VK4cyZM2jUqJEOqMZFloHVmFWaf2SCuOiuWrXK0aakvCAgCDgBgW3btuk5Sxu9kSNHYuzYsdi1a5eek6dOnXJCC66rQhgg12Htopb80HbySxgXtAPz/7ELadY6o5xT+M/nPyPr+otGd+g6c8GP2p1Hoe3FL7EjqcC9Ky81Cdea34N+jYsxNRQtKQXlHYz23QPxTfSbSEi3APmpSFizHolFVGDZ+OGNp7DWbwzGda4Jc3YeLBYv1GrfHYHfROPNhHRYkI/UhDVYzwuNugHUatsT9X5dg7iT7I+C2ZQPS771gFwEqTRTLghYLBasX79e2/YwiSITKJKysrI0k8MFNigoCN26ddNJFo0yDLJGxoi5iIQEAUHAtQjEx8dj9OjRRSS2derUwcCBA5GQkODazpSxNWGAygigO17u0+hBvLfjHdy9dzL6DJuG+YvewML5z+GZVzcgp6UJ+75OxsXEHdh76hx+2rkXv53/CTsPpMA3fDY+jG6JtVHz8dH/bsDbb/6CsaueRZNDX+Dr0xdwZOc3OJmWhIRte3A69Qh2xKeg/fOr8FTwctzVqAnC+sxCfOshCCuiAvNFaKcOMH00FgPH/R1fmgKQuuVNfOz1OFY+FYzldzVCk7A+mBXfGkOap1nVfRLoNh8rHs3G8717Y/SUZ/D+T9nIOboZXyUVxCNyR+ylT/YjQBdaSnzo9k47HzI0ht0P7YDI8HBnSWKofaPM8ePHERISUiQnkf2tSklBQBAoCwK0xztx4sRNVXBe8jdPIokE7Ul3y+G+5iMr+RgSz+YhpGVb3N7AH/ZwvKa04zh6yoTQDm3RyN+eKyzIvpwB7+AQlFzcgtyMDOTXDEGAjxk5uV7w9yvwE7NkX0aGdzBCSr4QgAU5qeeRUaMB6lazwNvf164xOAyVXOByBJhUkdFjL168qOP+UKpDm5/33ntPJ1NMSUnBY489pv+oEhs1apSW/LBMYmIiNm3aBGagFhIEBAHXIcD5ynlL9fWYMWNAm6BFixZpJwXa9Hl72/POcF1/S2upmG6jtKLym+ch4IOaTdujW1PHeu5btzW61HXkGm8EhISUcoE3/IKN36vB38qD2TsgBMYvJVfgDf/6t6EcQg6V3JycdRkCtWvX1gEO6VFiTfXq1QPtDLiwvvvuuzrKLO2CDKLUiGH4KQUSEgQEAdciwPm5efNmTJw4USdDzcnJQVhYmJ6znsT8EDWRALn22ZHWBAFBwAoBJk986aWXwGSKlPgwqmzXrl11iH0W429UhZHpoXqMZWhoSSPogwcPasNoq+rkUBAQBFyEAOfkr7/+qmNytWjRwkWtOrcZz5FVOXfcUpsgIAi4AQJkbpYvX64NnSnx+dOf/qTVXzSEJtEwmmVINIamUfSyZcv07pNeYUKCgCBQMQhw/lHy46nMD1ETCVDFPDvSqiAgCABgCgwuon/96191LJHffvsNDRo00LF+eEyJT8OGDTXzQ8Docrtx40YdgI3MkJAgIAgIAreKgNgA3Spycp0gIAiUGQEGP6S7OzNKm0wF4RcY64fEAIiGYTQNnrds2aKDJu7evVtLgsrcuFQgCAgCVRoBYYCq9O2XwQsCrkWAdgOffvqpVnudPXtWe3GRCaIhdEBAAO6++24dF4jutAyAOHXqVB10jeJ2X19f7NixAz169HBtp6U1QUAQqJQIiAqsUt5WGZQg4J4IzJs3D7Gxsdq4ma60e/bs0YzOn//8ZzD2D3MK8fPkyZM6ESpVZMwIz0zwkZGRhRGj3XN00itBQBDwJASEAfKkuyV9FQQ8GAHG7hkwYAAYK6R+/fqFI/nxxx8xePBgnD59WkuBKCViclRmmq5VqxboLu9p7rWFg5MDQUAQcFsExAvMbW+NdEwQqFwIfPLJJxg/fnwR5ocj7Ny5Mzp16gQjwSnVXYzxQ+8ShtgX5qdyPQcyGkHAXRAQBshd7oT0QxCo5AjQzseW5xbPM6CakCAgCAgCrkJAGCBXIS3tCAJVHIFBgwaBUiCz2VwECYbWp2dX3759i5yXL4KAICAIlCcCwgCVJ7pStyAgCBQiQPufZs2aISIiAozxQzpy5AiGDx+OadOmeVwixcKByYEgIAh4JALCAHnkbZNOCwKehwBte+gBxsSmHTp00HY+Q4cO1QkVo6OjPW9A0mNBQBDwaATEC8yjb590XhAQBAQBQUAQEARuBQGRAN0KanKNICAICAKCgCAgCHg0AsIAefTtk84LAoKAICAICAKCwK0g8P+/XDl5DTmIlAAAAABJRU5ErkJggg== />
(a) What is the conformation of ring A? of ring B? of ring C? of ring D?
(b) Are the hydroxyl groups on rings A
Question 8
z+8UEv6nPaxGoMg6lVWWaUtauvVjBCrzUKJFlLNkjWQNZA1UE8D6gqh2C3FA7RY1Ng2afPf+973pgKjeiDI70499dTgblN/yGrzUni5h1ioBtxPf/rTRYZaPUu23rX1te05db6vPbG+d72yxXbZZZdYffXVi4QHAMcL8PFOgB8YoNY+Fk9PMYDtuPteywhZ/4eP8Le//W1R4fStR/4YV09aNzZeZtZ23Hc+RtZA1kA/08CZZ54ZSyyxRHhvxpWuMCOgI4vls5/9bLH2n1omCjOqSeT9rrvuir/+9a8F66TWibFJZev+IsDdNddcU7gYf//73xeusd/97nfxta99rb/cYr6PXqQBxRPFCe25557x7LPPFgAI4FlwwQWLau8Y3Zlnnrkomrrddtt9YB+uW/21XdIrGSGB0d///veLBRU333zziBgfN/xg19jp4L/G/3LMdLuefT5O1kC/0YAsMXVGsMfNgCCD6VprrVUEZLJSDc6WlqguzGhQ3n///ePtt9+OO++8s2CcDMZ9Xdw/tyEXhXs27oqvosMtt9wyZp999iKolYswS9ZAuzSJG93xAAAgAElEQVSgr3FZlwUTyy3N0EhMbvl7/6d9xAelZIjqfVr53CtNGrUCKOSGG24oBqjJz/8lTvn98/HiuyfGZU99JXZepFdediv6z7/JGsgaaIMGLJfBgNp+++2bOpoMFTVK1l133aIuUVqhvnqpDvFCtv3sZz8rqPtTTjml2F8gdl8Vk9FXvvKVwrKWqgwQibv4/Oc/H9ggJQauu+66+OUvfxm33XZbEb8x00wz9dXbzdfdizSgv8kS07YwstxgaW077RJLpF/OPffcH9jHeoKyPxtNeGjktnsdomBxoaIFNrLUIibGk3++OoYu+6GI2/8ZJ5/3YGx3+MgY2sjd5X2yBrIG+r0GuHW4wwRZWpG+UWFV3nTTTUUMkUG4mcKM2BJg6OGHH+6R1bEbvadG9zP5rLPOOkW9pYMOOqgobGfsHTVq1NRJSUFFmXbAj0mLfi+44IJiwmr0PHm/rIFaGrBchqzERRZZZCrIBoa0MS8FFRM4AswFUXvZJhlCSQwus3ZJr3ONnXHGGfH0008XabDFTb49Ji6/bbU44uQdY+GIeOjs0+Nfr7Xr9qfvcaTmagzZypq+zyGfvW9rAGvBnfOd73ynqRsBZJZaaqliYm92FftZZ521GKyBiL4oypKIgwLksD8kFbIzESUx+ViGROD5Cy+8EH31ftP95PfeoYE555yzSGrA6lhUVZC0tkbqtUP7YH4VQm13AlWvAkLjx48vKkzuuOOOscwyyxRKmXDHpfHoGl+K5VbZKb4te/W538ZJf/lv9OVQIf723XffvbBeVcvcYostimwV1DsRNZ8KSaEJk3zjG98otluht5ZMfOGOuGHMK7W+inj9kbj+1ucie/prqydv7f0awPxw3QhU1m8MnDKcsEEWUF1xxRUbvolx48YVx7GoIykXXUyf1ScSk5BiEar30W9Vte5r8TPiqY455piici+dNlLI7qqrrorjjjsufvzjH4dA1yxZA13VgJg7CQjmOPF2nbVD7dZLP//ud7/b1dNP8/teBYRYHgaVVDsgYlzc+Kt/xfh/nRIHHHRuPLXoYhHxWvzphN/FE304TlFBqJ/85CdFqq+S4RCwpQIUgLvnnnuKRqGIJClX1E7BZRpDtbz10C/joNP+HQstOkf1V1M+D1skFn3mrDjw7PvifWhVe9e8NWugN2kAEyGIV9VoxoA4IPEstuk/+gwg1MwErQCjlPmvfvWrxa2K9ZEmXy7CaD2jvffee5pt5X0cQz/Vd/uS7LfffkUxO6VJytJZITs65spIDFL5t/n/rIFmNTD//PMXRr/4O9mJ6gaSWu3wvvvuK2LX9HeV4aXPt1N6TYyQ4Cd1PMQHURCZ9NSf4uIZ9ojTT10/5gYK/rdGPHfdJnHZ6JPirDt3iONX6Xup9ILAr7322sIdJihcYag33nijqFHiYVsVm3tQam61ywxLVFNeuyUO3+GiWPqiK2LxmWvuERFDYsRGu8ZKX90kDl766jh5rTnr7Zi3Zw30Gg2ce+65hcuLC1msgLo+5awwsS76zcUXX1y8uMkMlp3JM888U2REGYSJxVqbiRFKvxGvgF3qSwK4WbBWvAXBQGPXuMTStmSMps9pH5llmOutttqqL91yvtZeqgFz/T//+c+CocS+zjHHHPGtb32rAOoSF6xMr3QF1pdRsscee0zT/9t1W72GETr44IOLCPF99tmnuLfJ40fHj7+9f/z5kdFx3UMTYnK8Ho/+8954swCCT8Qpux0alz/d9xw9anQISlxooYUKEORmxRvw2avkessttxRR9I0/4EnxzGWHxNnjV4mVh1PO5Hjt3vPj0H2PiGMP2zk2+NJ2cfS1z0VBoA2aN0at+Xacd/DvYuykxs+Q98wamB4aOO200+Lb3/52rL/++kUq92qrrVZM2tzmqZia2BXACLMDABlMGym9z8goF2VrNkaIPvxG+rl4h74kxhnBqMBNegE+/ifAT71Cdlg3IQxZsgbapQHgR1V4scGyyWSLI0UwQ1zXJ510UhHPpjBqu5mgdA+9ghFiiclG+OlPfxqzzTZbcW2D5vpU7HPlczEFFk253KU2OTT+vEnt+BiWoeBjdUB6swA63F0G7LIo6IaqZ2FCwsSgY8CS0ULuv//+4n3aP6/ErRfdHK/OtV0Mt9vEJ+O8Hb4Zx8xyZjz8ly1ihlWWif23GRqrP3p2rDXb4Jh7kXnjzdG/iVvG7RQjhk97pPwpa6C3aMBSGVxff/jDH4p+jcVIKe2pyGHaZtzwHWDCbSwl3GeB0LUEA2s/KbqqRT/22GPF/uk46bjlgoppW3kf6eX6LDapLwm22UQjIwwAaqaQnXiOMiPXl+47X2vv1gCArt9PD5nujJBgPQMeK2+HHXZoSgfAjwArcQPDhw+Pe++9t1gfqKmD9PDOKY6heh0fsQYAEveXwTWJOAQAqDYIAnxejMefejMGzTJLFBU+Bs8f6+59aOy37ciYMPrvcfdLEfHS2Bj3Hnk2aOhsMeSdZ+ORF95Op8jvWQO9SgPGhB/+8IcFGyRxQoE1Ul3kMG1TfC3tg8kQeKneTxLHw3YI9EW1q01irAGULMZa6ziNnAsTJG5JEHVfEtdbLgbJKGu0kJ2K/4mN60v3nK81a6AjDUx3Rsjia/z6AE0jJeu5lQQ2CtiTscFCUQ/jhBNOKAZKVmFvlhT/JG21LGKkMD+AEqowyc033zx19Wu1S1JAWfo+Bg2LOWeJmDxpclSKjYNj1mFvx+1H7RJP7n54LCm4qhTCUJk8MSbF0Jh9lvYGm029nvxP1kAXNXDppZcWLJC+joHprMhh9T7/93//F4ccckgRQI1mN8bILuOOVhtHPIy1yICgBJgwSNXHwQhJ4AAUUkHFtI8Abm7uBKS6eMs9+nNrPKnCTc/WXmu0kB3jzTh13nnn9ej15pNlDXS3BmaoMJemk2A+PvGJTxTUMjBULxjYgCjNTkAkwMT9tfbaa4flN1huvR38lNXLBcjKRS8///zzU0GOgVtKq3sRTI2yx3gJxJRVRr7whS8U6wEJGFMDZYq8Ebfus0ysccMB8ejo3WLEq5fHRh/dKC4fvl/cdtc345pVl40DH/9C/P65v8Qmc0f899drxML7Lh1/feyc+MwUL+R7x8lvWQO9QwOrrrpqEXejDzQj3F1cWFjUxx9/vOhjirICP14m/fIYY1zBJGOJLLbajAjgZKRYE6m74haauZ5m9zV+igWytpN3gdIAIuYsfXbM8jZZq5dcckkR3Nrs+fL+WQO9WQPTlRFiWWA4BDeWBygKS+AnMT8J/KhlAfwYwPqiyNYQqClOgVUqSFrWi/uig5133rnJ25o1Rm63fXz88rti7JsRI4YMjyU+IhXk5Nhqyxdi1NAhEe88EFdcMzY22WLeGHv3S/GxbXeOlTMIalLPefee0oC6PYAJo+Dqq68Oad7icHzG3Oj/3tO2tA8QxD3OcBBzhwHCetQTTMgvfvGLYmFVFamBmkbOxUABggRz9kUQRB9igwSmYqAtMwII0Vs5c8x+gJD7lDoPY
Question 9
ObU+XqtKW/vyxqYbjFCXFoKA3L3KOtOgB/F0rbddtsC6Gy88cYhzRVIMEhhStC6fRUEuUdxBeIZuAGt38NSVddD/SQUvOw5IvA7xRMVGyKKlML0f/l95o/vFads/r+47JZxMXnYp+P4e56Lh8c8Frdd8Yv41U1j49HH7oyfbDEiJr98e1z2+FfilANWjmHlA+T/swZ6kQaMDamMvkm4XNCwoyKH+o/6QoAKd/mrr77a6V1tuummxWSfJnwuNCKOpvpcxh3XYzu3PFalr8pnPvOZwsUlXkqVXo4BgIgejMGMMq+ddtqpYIGAIKCSXrNkDfQ3DUw319hRRx1VsCGKoaGxE/MDAHz2s58tCiwZpPoy6OmosaCZBW9iw6zwjAkCioj0VGXHie2pnpDYKBkuK6ywQkglnkYmPhvXnHF+PL/2d2KbkVNcadN8//oD8etTroo5tt4zNhgxZJqv8oesgd6kAbWCTNRiUritUoyQIF1ghyGR4nZsq7WPRUTt02gWCoDDMEv96yMf+UgBdFRUlsgB/Mhu5cpnmLm+/iDip3bdddciTZm+1DXjst96662L2wMIGW3qORmXs2QN9EcNTBcgxMKTsbHYYosVKazAj4ElxfzMN998/VHXPXJPgqYHzViD6Js8KSbFjFHrqx65sHySrIEGNQDYqM/DddyKYDfOOuusYgmJZtckEqsI6IwePbpwXzs/QCbFXBC2+KX+JphngFGBV8xPWmjV+AwcYuZzynx/e+r5fsoamC5AiLWB8VhjjTWKCqWYnwx+yo8l/581MHA1INNLEUUp9Gr1NBK3U94HuywrE5PUSCbqwNV0vvOsgawBGpguQMjCidbxEfOTJWsgayBroFoDI0eOLECMsUJgtEBoK8xXFzm0TeXZtI/9MM7LLrts4c6pPm7+nDWQNZA1UK2BGj6U6l3y56yBrIGsgZ7VgLpg4nUAmlQssbMih8pxiG9JxRN79orz2bIGsgb6qgYyEOqrTy5fd9ZAP9aAmlkpVRvAUXUd61Mucuj2bVPkUOapGjf/+c9/CiCUam/1YxXlW8sayBpokwamax2hNt1DPkzWQNZAP9SAoGlZW5tttllRSHTFFVcsqiBbXFWlZ0HRyk6oiWMJGkttyILKIKgfNoZ8S1kD3aiBDIS6Ubn50FkDWQNd04AsLSyPuj1nnnlmEVuonIQaN7KdgB71fNQPEleUJWsgayBroFkNZCDUrMby/lkDWQM9qgGgRwq3l6KrltLYa6+9CjD0q1/9Kqd29+jTyCfLGuh/GshAqP8903xHWQP9VgOWxVBkVfG/c845py0gaNL4e+KKy++Ilya9p7YZZoyhs38kll11jfjEgjNH3UDKyePj3iuuiNvHTY7Zl1ktFnvhX3G3/5dbPzb+1PBo5+A6+eX74srLb4sXJ84Ycyy/fmw8at5oadnk1x+Ki069NN798h6x1cgPVd3b5Bh/7xVxxe3jojLnyPjKRivHPC2dpMnmN/nluO/Ky+O2FyfGjHMsH+tvPCrm/cB537+2ybMvF+tv/KkY3pCCJ8bzN10Q51/3fAwdsXpsvsUasUBH9WRLz3TYkl+Mr66xQMfPsbT/+8/99XjoolPj0ne/HHtsNTI+VLcBNamntHutZ9iQDtMBar13fM2Tx98bV1xxe4ybPCyW/OJXY40FGlL+lBNV62jUTPFg6jfd0Fdq3V2n2yy62tNy5ZVXVj73uc/19Gnz+bIGsgb6iQb+8Y9/VGaeeebKxIkT23BHEysvXrdHZeGISgxdu3LO/Q9XLv/OIpWIuf+/vTMBi6rq//iXAZRNQRTBDVSQRZRU0FdcUFL7p1m9mWZpab6a5KvmimiRC65kiqaJuYWGpZWZ+waK5QK44QZGQKCyyzoDyDLz+z/nDjPMDDNsJurbuc/DM/eee875/c7nXOaeOduXhq27RUU6LUgp6+AoMgfI5qMISlKe/0ZinWkaekNKmb+8Rc0BajfjEknqkU35/YO0cqu8HOKIydQaIPMxJyhfSx7SrIM0yhyEDrMpsj5GtORVnyBp5i/0VnMQ2s2gSzrsKn2z+Yh+qyPgouv+5AIjGrp9N71lbkh9t/5Vq1t5YZPJBiCLsSe1MlLPQPUZqKx3cQRNbg2C+Rg6oQ2yegb1vtJVh3VhqNOYNp/L79PBlVvplvAPkEdhk20IsKCxJ+tbKE1Gmtc6vWq0G393W7XWhhePwAlwApzAkxJgSvJMU4wtsX/yQx8WnZzQimVk1Art2jnC+91X0Ra5OLNpD+4W67IggrGlJYyE26rnuuI/SXjD8pcVRGH1OxOw5Vo+ZADMPAPw454QHPjSG+Za3BEZW8JSXiAtd59eUF3s1iWOuocVeBj+K+JgiGZWvTB5WSD8hrVRj6LlysiyNUy0hGsP0lIvZp4I+HEPQg58CW9tkLVnVOdQXXVYfz4qJjV9lhUgavU7mLDlGvLZgwMjWLauOxWVnAFoMtK8Vo/9LK7q0b/1LNzjNjkBToATqE6AiRd36NABt2/fFuR6qsd4khAZSrLSwCRbbQYMhJ0RIBPfQujaPfjL1BSpF6JR2m8e1vgOhRZVP92GZWLcCl2LPX+ZwjT1AqJL+2Hemnlwv78NvssP4WGLwRjrHIsdP9wEev0XW4P/C9fyKwievxAhsabo2VOCUgCGOiyU/rUfn316Gk26tUdBXCpcfP3RPmg0FkeKoZ+7FvMCizDa6CdsOPIQFtk94DnXASl7l2H1OUKr4jhkv+SL9R/rKXOn4nv4+Ytl+PaONV6btRBTvWyUw0SyvChsWbAChx5YYMj4bojdthc3qAd81s2C2e4F2HihDN2nB