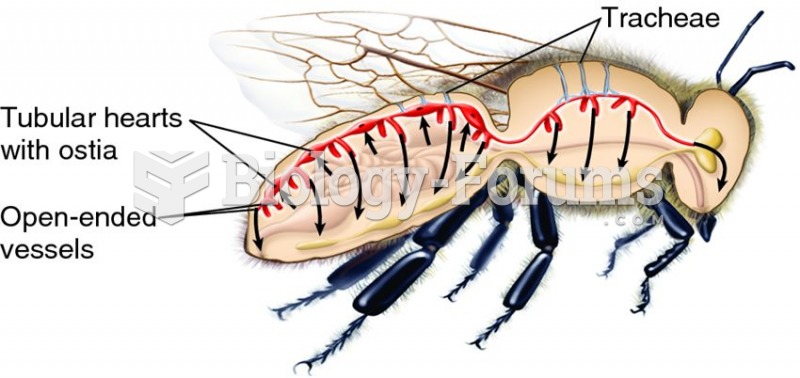
Suppose XL > XC. If switch A is left open and switch B is closed in the figure below, what happens to the phase angle?
 Question 2
Question 2UQRiSmuAJLCRbITZ+jpj9HRGWNX+x5SmSQnTZ/K/LPP4pj6atVnSZ8veCil1z6dOOQhccDVNO/9FYiGsYMRYrEuJaUot9xcxLx0wQ/adDHTpaTMLJ7Rj2GGMDwrR4D7zOB+ey3AOOkMwSKbq78+ifsGGmh9O876Fb1kUwkWfGkyJZNNpfN0swGfLIQTTJNgCAZaYNm/t7PpuR4sJ0jdKXDDX00iXGaQSSi389x1BUE/bUOm31VkGS7OBf3st2cDvoSvAAAgAElEQVR6p0ZAIzBeEIhGosptWNxmZW3ISzDSfyEZSQCZSTuYURvXz4Sbe9gdvLL6UkvWC9Lc2kljUwfRaBGnzZtLTVW1ejQefPRoYeOJCkqp3RyKCyMsuugsTj/peF5/dxNrNm/j1Xc3q4Dy4uJCisMmoXBYOSYIb0ous2QyoZwMeuJpJFFkUTTK3FnTOWvuscytn4RlmX5KfaFRsVMfjkFIKpqhAFE0IP8YYEeiBCrLGOjcBRkX0/L1dvlzVe1kPALiWy0FYkxReeX67L2nJssfP9S7sGYmniVYYXHDX03nkb/fSeNbGbY9n+Tuhl2cfU0V088NEyh1CBFAiD3Wn2HHqh7eeKiL3s1Z7KxJ7WlRPvGXtQRqDVIDeS+2nKhIGtMLqxsj1plResmCKh2jMtSc6P0agfGEQCgcorCoUCV6VMb5XOdFVSSkMpBOkUhlMSQ55OCMHbkFT1TslhUimXJoaGqntb2DmroaTpo3j6Joka9rkVXc18GPKjRqoZcAbVPWV6WYp7a0mGsuPJOPnzmPHc0tbG9spamji7bePrr6O9Xzsalcpk1ESqufNImzy4qYXlfN1JpKigtzTgSqOJejFmU/Gn9Uu75PY0OSihyVz1QZMG3KZkymeeUqkt0O4Tpbla7Mt2Qot10RycTvTjSWyhHLnwA1ccOjRN/bzCSb8iioNbjhO5N45mfdrHkmRs/mBCt/3ETkfltFw0dCQbJJh+6WLPG2NOm0hRfNcvL8Mi79wiQCdVncPoOAGMPUDZBjSBESRceKQ3dTimBRlKK6Kfmh6HeNgEZgnCKQl0rKysppa29X6Vok/Up+fzgcUtHwvbE4dW4phpFPA+W738ryZVo23X0Jdu1uJRlPcdzsYznh+BPI12pRK9lhIBQFuTSu0sP4cS2DpyEaDjN35gz1Emkmkc6qVPdS+VHKyNi2QcCyCQSGWNINUXUN0vQNb0ke3IVhfx6iB76UIdcVi4S81x47g/X3xehtMYnUm4pJ/W/z11JU/0G7ifo6/13+2A9/T8dNzJIIV3wTZpwa4M2lA7RujzGwA/o3p8kGkso4ZVoe0YjJpNkBTr6+lpMXFJCxJGI/hI3YXuTa/vXFgwyjAC+YJhtz6NkVI1o/k0hF6Yd3SB+hEdAIjAsEKisrMLaYpNNpZeAWUpGXkIpIK/39AypAMO/FKnYJyRhsGAHaOvrY1dCopJVTTz2V+npJsujHfeS9rY4ECHliVK5ehqE81iK8l1pK7Nw+TwhR7uud+1H3d0hSyXckT2jVJ84iZdq0bh9g2pllJMQA/r7Izvw5o/EubsokXbIBi7lXVjHz/GJ2rY3TtM6hryWNl3YxQh6l1SaT5pQx7aQCwhVZEskUVjJK0DNwLHES8D00pE8S2+oZaYyAS6wR2rcOMGPRbCIFUeVX5ldjGI3e6zY0AhqBI4VASUkppSUl9Pf3q+y7EhAprrtiYykoKKSvp4OBWHJvbkG/OqxLc2sHDU09lJaXM3fePCpL/YdNWdCP9KY8vXL98Pvju1GJ15f4xMo67ZvdRTWnkhzudTn+qPt+YFLJiWLSqdrTT6S0uoJdqzs5dXEFpiEVzA7f5hlS08DDyAZIZh2sqMlx55cw50I/BYGTtZRIaokmzs2SEUNVTNyebRVJ7/O2EIrALTeFxNhIRL3ULwjRsq2HVLdD/fknqUFI7YN8BoHDNyrdskZAI3A4EBgsRYjNoH7yFFaveZuBRILK8vK9pFJWWkR/XwdtXf2q9K70JesYbN7RSn9vH1Pr65kzdw5SETK/DW47v+9IvOf7kX/Qlz4Itewbtpj7dvBBH3FnD0wqgzpTUFfNpNPOpvnVJ+ltHaC02saV/NCHcfP5N+MHIWVREaLqckJ2hqSwd8DPqKCIQ5niVfp8OSr/dJF/FzfoIIbpEXBg6xs9GCWlTDvvTHVkQLPKYZxJ3bRG4KNFoK6ujp27dynbitgjJKZEUuIHAhbFxSX09PYrwjFMg0QiycBAgjlz5zFz+nT1hL9X3fTRdntCXG3YIS/CiMdddSkdrWmaXk9iSeCPWq8PL7H4ksb7sBbpTsSkPF/s/fpAfRGdqYsZMIk1Z9jxuxiTzzmVyuNmKYlLpBi9aQQ0AhMDASGRuXNPVIWwtm3bxpYtW/Dft9HT008265GVOhySYioc4vTTTueYGTM0oYzC9A9bUpFrzV5wHpXTprHut3s44YoKDNuvlyzxKAdazkehn6PQhNSGcQiGArzzegc9DSku/e6VSs8q5CQeYmN/DKMAg25CI3AUICC2BlF7nXPW2TQ1Nfrqr1w+L3HdFfVWNFKA57hIapfaaj8oMC+h5N+PAqhGfYjDJhXxmy6qq2XO9Vfw6k9/xu5Vdcy6IEQ84ZeqNPLZJ0e9i6PVoIdlecR706xe2kf5CVM57urL/cZVloIj6zExWqPU7WgENAK+rUFwKC8tVa/9YVJeVqZ2S6nd/LbXbnG43IbzF5rA78NWfylXNuDkz32SQGktr93XhDMQxjRCmEoXlddHyftYe8lN42EVGmx4aoDdb8U45Q9vIlxeOIGnVg9NI6AREARE6si/BiMiHmF6G30Ehk0q4qXmuB61s4/hjN+7ka3PdbHmxW6CUXFlE99oaUoUSPLEL5/H0svACpn0tRm8+usmKudN57RP3fhBk8zo46tb1AhoBI4wAiJ95F9HuCtHxeWHTSqeKb5Vvph49pd/j4rZx/C7O3fS2Z7EiJgq/5flisf04UlhMOLZUPnBMphBj1d+3Urb1n4u/foXKKyqRFJF600joBHQCGgERg+BYZOKmLGF7T3XpWRSLRd958t07Ejw+k9asJwSApZYXWw8U2qTSJ55X+V0ZN+laJdHqNBm629jvPWrRubetIiTPnWtStw27MGPHt66JY2ARkAjMKERGP66qrJnSrIzv+bySZ+8ljM+/2nefKiFNx5oJRiycSRJm1swzLK/hxNX349LaC0cDtK2Icvyf2kiOnMmC77/5xiWpWpEjnnfgsMJkW5bI6AR0AgcBgSGTypiMVFpAnw1mCzbl3/3q0y95BxW/utm1q7swS6xMKwUkhnMlBVbVnW1vss/H81Lcnu6plxfCMUi3pbhsb/fQqzbZeFPv0n5zOnKj8DPrKw6dxhg1U2OBQT2yspiqD3EDilD7yG0sj9D8SF2SZ+uERiTCAybVJShSxV18TNoOi6Ey0u57ud/R8n0WTz2vS1sW9lFuMBUEovrSoEs8VjOZwL9aMZveh62YxAodIl3wZJvb6ThnX6u/Je/4vgFl/mdMGUMuQI1H0239FWOEAJCJ6NCKPJAdQgNCanIpsnlCN0I+rIfGQLDJpXBPVI/D8/Fy7qUHTuLxb/+AXbFNJZ+cwtrH08Sipo40TiulcFyxBtMzhhNN2Np7/1t+n9LFclQEbQ3ONz/f3ay41WHj//jdzn9D2/h8GYrG4yQ/jwmEPDEB1GCXoUQ5P4YwabquRkqSPZQwmOVTVL5sOQk+BF0RZ+iERgPCIyIVNTAVHJGl7TrMem0U/nUAz8hMnsGS//2XV67s59ANoIdzajaJe+5Go+Wu3H+oTHXnifvUhnYIlQYYvvraR64YxM71/Uz/yd/xoVf+X0cWVc+WqFpPMz/hO6j5HqSsrI5HezIxprjo1RayiiMfBNJX7Z4PI7km9KbRmCiIjAiUpGfhGVYGLbtF8HyoO7keXz6wZ8z7bwLWP6TzTzyrS30bLcJlUvtecnVJblQJF1+FsN0EYli5JuJRPAbRlJFw0hfgkVCGiYv/aqJ+768hkR/Mdf/z/c574ufVZeR37Ftjmi4I++mPvMjRUCputR95t9b3W+8yc6f/xeOTP4IbzcpwRPfvp2N//gjRu7Y4SmX+1R3Nxu+832SifheQVu8E0fYtY8UW30xjcBwERj5KqsCilQ+NmUUl8DIsukzuenhf+fCv/gca1+I879fXM3Lv+kjM2AQLUtDWEQFW3mH+dGsohKTn9TBvCTbsOQvFt2GQaAAjGia7S+73P/VnTz1j1uoOfNCPv3ELzll8fV7f7Dq2VA/IA73vhiXx8lziggEmZwk0PzQCjb8+Jd4hyAdyC3TseI5dv3w3+jb1TAiXOTulh9ax5ur2PHjX9L76mpFMnIfy3OWJpURwapPGqMIjJxUBg3IM2WRd1VytlBRCfP/719y2/3/SPHkk1n2vY3c86UtvP1QBqffIFwQIhAOYqqsY0Iqw13p5Tg/VsaKgFlmYHpF7HjTZem3mrjny6/TsCXLx7/3F9z+6H9Se8o8MqLz0vGNg2Zqgn90pWCRv4Ane2J0/PZp0lu20vbU8yMeuOO67HrsceK9LbQ9/OiI2snbYtrvfQw31UXDPQ+puz5reL6X5Iha1SdpBMYmAsNOKPmh3TdymX7lscvwOH7hIqaffymr/vtXvP7zB1nyN5uYPMtixhUVzD6rjupjAgSKs5ji+yvq6qyB61k5e6ooBYRETAzLwbA8TMvBlALBSZuuhhTNb8fZ/OxGtr3chxss55Sbbubcr/wBVaec4PNIViq9SZ98b7UP7b8+YPwjoNRcrlLN7l7xDL2bN+PaDrvuXkLtNVdg+48+/kJ+gGcZKS8rm9hBel9+g55XVxGxK2i+7xGO+eM/wAyHUSVoc8fsFzj1POO3I0Wj+nfuov23zxKMltK88lmO27mbgulTMTIehq4Ot18I9c7xicCokIofbe8by30Y/F9suDjKeV/5Y0685QY23PcYa+9bxht3buaN/15N9ewgU06soOrYUsomByisMggVCcmgiEZ+tF7WIpsyGOhL09WSoWtbktZ3B2hZ202s2yE6vZ55n7uBM269gbqz5/kyj+ci5UGxVUHi8TkrutcjRMBQc5/xPFrueRDLAbOogD1PP0/Xho1Un3CC0jWJ2SWnIfvAdcTC4ar0PaZSpe287xGcWAKrpIjOdzbS8vQLTFm0wLcRKjl/CHZSsTEurulX5mt46An621oIlxeQbmii6ZEnOf6OPyLnY/KBfugdGoHxisCokMqBBi+/z+Lqas7+0z/gtM/dTvOrr7Fh5YvsevFt3n5iB6n7thEIOwSDDpGSCGWVZQSCFvGBGAO9A6RiLpmEQSYB2VCQ0hl1TLviPGYtuJSZl5xL0eQapfIQtYelfsjyI9bb0YiAyuVmmvStXkPPc69hRIOYlkV2TxfN9y6h+jtCKgairj2Q2lWcQCzLINbSROuyp7EiYSzTIpvO0nj3A4pULMMU+hlSeSvXMF153DJJD/TT9uATWFKi1rMI2QFf6vn8p7AiUd8+OGRLR+NM6jGPZwQOO6mIKkyM8hLpLraUaZdcqF5eyqFz+w72bNvBni3b6N61mz1bW3j5tTfIZJPMPnY2U0+fSaA4SkVdDWWzZ1A8ewYVs2ZSWFGqMFdaM6ktL7YTcfAZ6vFzPM+Q7vuwERBPLXmgaL7/cQYGOgmWlhLMGDgFNp0PLSPxlS8QKiv3E4mKNLufhVzJHbmnkvZHVpDcvYNgUalyDglGQ3Q//Tx9G7ZSdMKsDzWw59xS6HjmJXrXvINZEMHKeniRIN3vrKLt6ReZfNXlvqV+CIFn2IPXB2oExggCh51U5LdimJK4JefkJT9F8RwLWVSeMEu9YL6CY/O2bXzzogtp7WrhV3/6t9z0qdv3C5OvqVZ+ZP6yYBnK3VNda79n6J1HAwKSIyHR2UXDskcJSE0GR8x1GcxIAbGNW2hdsZIZt3wSQwJy988pimjEBuJkEjTevxQvEEL+jnspCq0QifYOdjz0MCf/9TcwhcWGIAM/pZHPTrvuX0o6k6XABTOdIRkOY6WTNNy/hClCKrog1NFwex41Y8w9kx3G8aofjK9XVj/AA/yAMqmU+HcplcGBHgPz5KF+z7k/8vsO40h00+MAgZZlK0mt204gYBMIBfCKCghmUrimR+M9j5N1sz6hfMhY2l9+jc433yEcDqiYqmhxOY6ZxQ6HaXtwGam+7gNygUjmlmnQs2UL7U+/TDQSwCGLM6UGW+x+kRCdv32Jns2bP6Qn+muNwPhC4PCTysHgkcuErMhipGk1DuZ6+tgJhYDk1Wq7+2ECRoBEOkHJ2adz/J9/mUQqQaAgQteLr9Hz5mpfulA32f6HL1/tvmcJdixGJpOk4JjjOPG7f0VaavMEQyTXb6Ll8af2f3J+r0jjQMt9j0FrhyIyr6yMk//h27iVhWC5ZNtaabh3ZG7K+cvod43AWENgbJHKWENH9+eQERicSPGQG9tfA66L40lxOOh6czVdr7xJpiiMkUlTf+3VTPvsp4hOmorjuKRjXYp0PtiMX242X6q8f3cTXct+h1MSxh1IUX7FRUy5fTHlc48nlU6TMaDl3sdwckXepGrP+zchlHgsRvPDy/EiBol4itrzz2fKdVdSc965JOMxnMIgrQ8tI9PXr04XrzPf8+y91qTlvarjvN73va9H7ZNOdDlqUB71DWlSOepvgcMHQL4GeJ5YRv1KEpHuSZpQf7VtuGcJ6f4YluNSOHUylZdfQqiwgNpFC8gMSKLTIM3LVhLv2LO3K9I35b7uyILu725a8gSJplZlp4uUljL5hgXKBFO/eBFmMkU4EqX9pZfofvtddYJwi+uKWX7fbc9TL9C/bh1myFJeaPU3Xa0OmHbz9QTtKLYdoH/jBppXPKv2Syoj8SgbvEk4p+c6qn3nMGT8zpPJ4PfB19efNQIHi4AmlYNFTB9/UAjIYqXKJhzAlnZQDQ4+2DAwrQABw4aeLpoff5pIIEA6lqTiqkWE62rU0VNuu5ZAtAzXDtC7rYG2JY/vbUX65hkmhmkhDmFeIkGbxKZEHIz+OIUXX0jpSSerpb76uuspmDwV10ng9HTTetf9qh1xEPANLO+JEvKp+TdLMLIZ3CSUnHIyNR87T9FfxaXnUznvNEgmwHVouutBPM/BNKQgw76b6VrKnVlcoyXH3Whv+bkxdV680Yb2qG3vsHt/HbXI6oErMhEYduzYwYYNGwgEAqOOipISJAfcCy/hNDSSjZjYwSiTbl6sbBridl565mlUXXAmrc8+gxkwabj3Ieo/exsBO6Dqm4j1w1U1dqDl+VfpXLOOcDBEJmUx9dbrleuISAyFU+qouPZKtv3s59iFxbQ+vpIZf/5lorU1qsy25G7Ie4MNrNvAnmdfhOIQyZjDnMVXYUUKVbbsQChCzc3X0LTqeSIFxXQ//yJdq9ZRfvpJKpN2njuEmES1137fEgY6++iYNY1+hHwOYBA6SISF9CWb89y5c6mvr987ZwfZjD5cI7AXAU0qe6HQHw4HAvIkvHz5cv7kT/6EYDCoLiGL2GhsKmuwqK9M+F6ginOjRfTFYlRefA7VZ52ipAJ58jfNIJNuvYbmp54iUGyz58136XzpFWovuQjXNbCMXKUdw2Lngw9B0rebFM85jilX+O7uUpdFtsm3XEPD//5aJUbt3baLjmVPMf2zt+GKmONkMYwApgXbH3yMVNcegkUFFNaVM/n6Rer8vCRSc/3HCf9kGsaeLlIDAzQ+8BgVp5+Ea1hIsn7TcTEtk6b7lvDKbX9C1DZ4wkjxC7cfS0hFuiOsM0KHFpkX2eQ9k8lw55138vnPf17t0/9oBA4FAU0qh4KePndYCIiEYts2RUVF6qlYTsrbW4bVwBAHyZoqGYnLsy61aUgnu8mks0y95RNYVq7GTu7cmqsuo+S440lt30gqk6H1riVUX3KRylMnVgxRPfXt2E7H8ucJFYRIxgeouf4KrKJorgWfDirPOo3ys86i67lXsGyTxruXUv/pGzHsIIbUGLIg1d9L64PLMQtDOP0Jpl7/CQpnTFftyFouPFAwdTrTF8xn23/dhVkQpnXJco7/+ucIVlX71SEtk2w2za5f3kPQ9igpLqA6ZRIKQEhSG6s8Z4dGKkIoovYaGBjYS/hDQK13awSGjYAmlWFDpQ8cKQJ5I7As9P/+7//OpEmTRolUPEnYoNRToddX0fM/D1B/1pnU3nSNeoofrCUKl1VSe/VCNv7TesKyiC97lpk7dlM0YyqO66f2aXrwEZyWduyiCIHKCqYsvu4DQ7bsAHW33cSe517GKgjQ9dprdL70GlWXXIhnWqIAo2n5SrLrNkOZodRxk25bvE87eeXVpFuvZ9u9SzBMh8TWTbQ+8iTTPvdpVXfIsCxaX3uD/tdXYReF6B3IsuAvv8RlH7sQQzJUiLAirDrCTQilsbGRO+64Y1TmYoTd0KdNQAQ0qUzASR1rQ5IFLC+ZXHrppVRXV49+Fy+5mPQf/wF2YRFeXhzIGzhyCVlqb76a7b/8JU42SV9bC+0PLaP4z76gntaTiQGaHl4GIYuBZJxpV8ynbO5xyrMsr/qSTotUM/XqBWybNZWBpl04qRStdz9E9SUX4qpxOjTetYSUncZNmlSfdiqVF569z3hVWS4Pys89g+pzTqPlhRdxgwZN9y1j8mduU1KIyEWN9ywlnohhmCFKpszkvDu+hFVSvE9bh/JHc3OzUn8J6R8tW95xRMZ7NI37o5zfvIr3o7zmAa+Vn2hZiGSTv/VrfGKQn2ghlPx8iqrlcG3BomJlxBZpIX+9/LVk2Sw/eS6TLzqXbH+KSNBm58NLSA/41UMlk3HfO5sIhsN4pk3djb6UonJP5huRdw+CFaVUXj+fQCyLHY3QsHIlA7ublJTS/fYaul56E6sghJsymXzD9diSSHLQ5hkORtbBCoSouflalU05VFjMntdfo+uVNxTJxZta6HzitwQKQlixFJM/8fFRJRTpTiwWU70SrPK/O5mrifx7GzQN+uNhQmDMkYqMU27qSCSihiw3vH6NXwxkEvNzeZju4WE1K6QiZFN7y41YZggrFKR/9Vo6nvMLeDXe8wSBZFrZW6qOP4GahReSkpYHPcTLR8P1o0VmLr4Oq7QczzRJNu6h+WHfTbn5vseI9/ZiZg0KpkymavEVfhOD2jE9C8MyVdTJpEXzKZkxE5L9uLEedt37oHIrbln6GAPNu7Asm0BROZNvu2pY4xzJQfJ7i0Z925HYWCb67y2Pkdj59Db6CIw5VOWGDoVCPPfcc0plIp4pehufCMhiJR5fL7300pE3BLuQNT1qLv84xSedQN/6dZiZOC0PP0rZnLl0PPcKRmGA7ECaSTcuJFhQJM5cOJaHlVOjSQlrVwwZHpSecirFl5xL8onlKoix6dFlTLnxalpWPEeoIKhiZaZ++kKKp0z1HbTyhhQ1lQaOGMldl4KqGso/cQVd//xjwoWl7Hnqafp27aDl0eXYBHFiDhULz6L4tJNVO4PtRKN1V8ji+vzzzysJ6Wj5vYnziLi65x06RgtL3Y6f6HfM4CCLkIjfMtH/9V//xX/8x3+Mmb7pjowMAZnTcDispBV5YDhym4PrmQQLI9TcuJDeb64mWFBI80uryHzze3i9XWRtg0hNJXU35Az0ovvap8+GHySpdhscc+sN7HliBW6BQc+mraz5+rdINTcpFZxXUEz9TX47Wc8hsDdA0kfAL/bo41F/y3Xs/OX/Q3JdJjq6WPfl/0Pfui1YkQKceIypN12rkqxmcbE/EB556IjK/PzqV7/iF7/4xaE3Nk5ayEtnck9ms1m17ugA0NGZvDElqcgEi6pE4hjk6UkmXm/jFwGZT3lASKfT6nUkR2KYBrajamQx/bqFNPzkF2T7e3E722he9hTBiA3dCWqvupji447xu6rqs+xLhCpNZG5X1RUXUzjnBGKb1mG5GdofW4kX8XBTSUouPJ2Ks8/GEcu+ENPgZvJ/5ghLbD01F1xIy7KnCRdGaH36VexwiEw2S9Fxs6lbeInqz+HUVYu7d3l5+V6X7yM5Vx/VteX+FBufrDnyWW+jg8CYIpWZM2eydOlSRSZ6kkdngo90K/JwcN999/H3f//3R1QFpuwhSOpHi6LZx1O54DJ2/fp+iouk5G+QrJvCCwaYctNiZQORPFyyzKhaXkOAKFH1tddfw6a/fZdg2EWCSJJWFjNtMfXGaxQxuK6Hpfx/979oSb8kRmbKrbfQuNzPfBwOhBQZOfEkVdcuIlhegZN1VZntfchpiH4d7O54PM7XvvY1brjhhqOKVAQn0YyIPSn/AKvXnYO9ez54/JgiFXlimDdv3gd7qfeMawRmzJhxxBcryc/lma78K1TBpFtvpP3uJ0iLikvUrgMJik47hapcfi6lrRqGoDzpk1ex4z/+k+xAH2YgijmQJXjMNKqvucKfM0kLpkL/9z+FQjWSyHLSgosoO+F4erdvxQ6EVBLJSFk5Mxd/QvVYsgaoHGP7b2bEe2UxFc2APNDNmTNnxO2M9xPzpDLexzEW+n84JeqxMD7dhyOIQP6HKuqvsbAZkjgy96hfe+E5FJx5PMTiimyctMnkxVdjF4aV1UId+SEqEdHOlhw7i5rLLiYzkFBRLG4yTd2VF1JcW6uG7Ldz4NFLpmW7tIg6SeUSS2GaLkY8TulF51F88lzV44B4ZR2mctnydD5W5ujASB2+bwUDLaWMDr6aVEYHR93KOENAYkcm33wdQiakM4Qm1VF/7cL3JZ4/8KAkiFHclOtuux4jWIiVSmMUFTL1ln0j6A/cii/JiI9j/U2LiFbXQjKD5drU337th52qv9cIjDkENKmMuSnRHTrsCPhewUy5/koKpk0j0ddL9cILKJg5i1zdrWF1QdKlOB7UXnIBhaeeSCLWRc25p1By1plKpTasRpQdX9yLoeT4ORRffj5OrJfIibOYtODi4Tahj9MIjBkENKmMmanQHfkoERDVVbRuCpVXXuynXrn5eqX2cgxx3B2GMUU6a0DW8wiEw0xffCVpUtTedC22qk0yzDZUFmXwXYzh2FtuIIPD5E9cRaCwZLg9+Sih09fSCBwQAU0qB4RHfzkREVB281z2/ZrrF1B+7kWUnHuGWsBVipfhDtrwA72EPiZdeRll51xKzYKL1Nm+79hBNJRzDqu6+BwqLl1A1TV+yv19QvqH25w+TuPGDXAAACAASURBVCNwBBEYU95fRxAHfenDiICkMpGnf7EbSPbdMbEZfhnh0jNO57R//DZWtMiPWPf8NCXD6aPkNhYJI4NHaMYMzv7X/0toUnXOLpN3CRhOS4OOiRRx+o+/R2jWTDKuR0ClYd6/O/Kgs/RHjcCYQUCTypiZignSEc/FMcAcFJthey4Vnkm1B25KvKT8TYjGdD0cw1+c8/s/kncpHey5hErKCF9wOo4kvcQvLaxElmGt4ypxi/LOMgNBSs4+DTHKCMnYOS+zgx2LcEjpvHk+Aadd3KC4EutNIzB+ENCkMn7mahz01CMji7MHjm3jJBLs/PX9lN35G/6lYDKRtM2OG75EzyXncOznPkXhvOPIeHK8955R4SMYpfCFch+V2va5LZ+iY1hckj9JRcabqFbyJxomfn3L/EEH+Z5rRxVeDmo6OUj09OFjAIH3flVjoDO6C+MdAXlyt7Btg1hTE2s+83Wan15JkBTFoTBe2qLn3TfoefdVmh96hHn/8ndM/eQncFxRjI1+/frxjqbuv0ZgPCKgSWU8ztpY7bPnqvrp6f4BVn3mDrpWPkkwEKL49AuY9LGPESgvpG3VajqefJZscwtv/9GfEZSgv8s/NlZHpPulEdAIHCQCmlQOEjB9+AEQUIkTDZp++Rs6Vz6LEYhQ/YVPc8b3v02wqFCdOBNofXg5q7/wTeId21j/vX+m6pKzsUMFB2hYf6UR0AiMFwS00na8zNS46KeBl82wc4kUrMpSeva5nPlP3yVQVEjKVTZsVfiq9vqFHPPNz2EEw/SuXsue11aPi9HpTmoENAIfjoAmlQ/HSB9xEAikWtpJ7t4lflTUXHU5dihK2pFUJA6G5xLOSi54mHz1fEJVNdjxXvreWXcQV9CHagQ0AmMZAU0qY3l2xmHfJF2746QRB91gcZFyrLUNB9NM41oOjiV0A164gEA0ihwpSRj1phHQCEwMBDSpTIx5HDOjsGsqCBVUIdl5O1etVoGAnkRaeBaeZ+K5EjII8c3bibc3i68YoZr6MdN/3RGNgEbg0BDQpHJo+Omz34dAuLSU8vPOkoxWND2+lNann8eWqotmEMOwsC3I9Pez7kc/w+7txayvo+a8U97Xiv5TI6ARGK8IaFIZrzM3Fvudy/47848/hVNVjtXRw7uf+RKbf/6f9OxooL+1g5ZnXuLVWz9L94qnyGAx5fdvJXrM9LE4Gt0njYBGYAQIaJfiEYA2EU6RWiCOSifiP1f0bt1GtGYSVmEIjAwmoREN03Ch7IxTOP173+KNr34Tp2EXa7/819iTf0YgFCbd1Izb360ygVVf+0lO/dpXdPnoESGtT9IIjE0EtKQyNuflsPdK8lxlsx5NTz3DS3/wRZ45fxFtj6xAqiPijSy63VU5v1DG9ymfv51L77mTwjPPJ+SESO7YxsDGNTj9Cez6Y5j1jf/D2f/zY7zSQrJkD/t49QU0AhqBjwYBLal8NDiPuauIB5aVdVj/Nz8i/upKPMNm24MPUHP7VQT8bFYH3WeRfrKeQyhrkbFcKj+xiEvnX0zL8y8TX7sJUinM+klUX3AGpccci2SflwQtIcf0c8gf9BX1CRoBjcBYQ0CTylibkY+qPy6Y4SDTb72K1W+9il0QIvbcK/S8/iZVZ50zol5YkkhSCleZEPBMso6DGS1k6sIFIK9BmyvJ8F2XgGGSNS2d+WsQNvqjRmA8I6DVX+N59g6l76KqAqYuvobieskgbBKPd9H8m8dG3qphYFk2tqRrEeHDtlQN9/01aGJimzaWYRLQd+H+INL7NALjEgH9cx6X03bonfYk6DDrEayrY8qihcQSSYLRAtofe4pEa/OhX0C3oBHQCByVCGhSOSqnHTwpeuL5KVNqb1tMqKQI07TpadhOq8rddZQCo4etEdAIHBICmlQOCb7xe7Kon0xb4t6h8sxTqTv3HLLxAZyQwc57l5NNpdTgpDqiGOD1phHQCGgEhoOAJpXhoDQBjxGXYlX9UMZmmtTefh2mYxMNhul54106nv+dSrGSdTShTMDp10PSCBw2BDSpHDZox1fDVYsWEJ07FzftYqT6aP7NA758YprgamIZX7Ope6sROHIIaFI5ctiPqSuHi4upuX4hTiKFVxKg6alnSWzZhmmKgixfgH1MdVl3RiOgERiDCGhSGYOTcqS6NOWmhUTLqrBck3RrBzvuf0y5Hbv6LjlSU6KvqxEYdwjo5WLcTdnh6bDnQfkJcyheeCn0Z7BDIRofepxUXy+WllQOD+i6VY3ABERAk8oEnNSRDElFuGMw9bbryIaCmKEQifXv0PHk0yNpTp+jEdAIHKUIaFI5Sif+/cOWYEhx9Jp8yQVEz5hDJpXGcz123LOErOfhuvJyEYlGbxoBjYBGYCgENKkMhcxRtl/ci02VDyzMjMWLCCRTBArD9L7wMnveWoNhKidkKQR8lCGjh6sR0AgcDAKaVA4GrQl8rKIMTyqswNTrryM0tR7H9fC6emi55yF/5IaBJwVT9KYR0AhoBIZAQJPKEMAcbbuFVLAMJHtLZMoU6hYtJBPLki6O0PbYb0m0tyN5Ih2t/zrabg09Xo3AQSGgSeWg4Jq4B/sR9ubekJT6m68lFAkQsgz6d+2icelyNXh7hLVWJi5yemQaAY3AYAQ0qQxGQ3/ei0DpuadSctF5eDFHxaq0/eZRspnkXtLZe6D+oBHQCGgEBiGgSWUQGPqjj4BUZMQOUH/zdaQ9g1AkRN8bb9Hx0is6YkXfJBoBjcABEdCkckB4js4vjVxe4slXXkHhsdNxnAypdD+7737kPd8vx1Mux9oX7Oi8R/SoNQJDIaBJZShkjuL9puchTl7hilKmXLcQYlmswgh7lr/AwI4dilikrLzKCqYN90fxnaKHrhH4IAKaVD6IyVG/xxO2cBxEDTbp5hswKyswjCBOUwtNDy5VZCK16D1xB1MHH/WQaQA0AhqBHAKaVPSt8AEEXAxFKKLaKj/xBGovu4BMbwI3AjsefJR0LIGNKMl0AuMPgKd3aASOcgQ0qRzlN8D+hi8JJO2Atdd5uO7WGwhZNmbYJL5mAy1PPas8wgypCqmz4u8PQr1PI3DUIqBJ5aid+uEPvGr+hRSfNBc37mA6Hq3/+xCe5+GZUo5Ym+qHj6Q+UiMw8RHQpDLx5/iQRxiKFFB++9V4aQ87EqL1hefpW7VeSSuSiFJvGgGNgEYgj4AmlTwS+v2ACEy99irC9dU4GCT7eml44MHc8foWOiBw+kuNwFGGgF4RjrIJH8lwXc+jeNo0aq/4GN5AkkggTOOjKxjY04nKGTaSRvU5GgGNwIREQJPKhJzW0R+UKLnqb7sVryCAGbDIbNlB+6NPjv6FdIsaAY3AuEZAk8q4nr6PpvOu4aniXGXnnUX5WaeSSiXJmC6t9y5VhbukF14uCv+j6ZG+ikZAIzBWEdCkMlZnZgz1y3LFb9jDsk3qPnkzhuNgRwppf+U12l9+XfXUFfdi7Qg2hmZNd0UjcGQQ0KRyZHAfV1eVWBTTQ/l5TbphPtEZszHTaVLJBG2/eliNxfBM5Q02rgamO6sR0AiMOgKaVEYd0onXoAggGcPDdD0KyquYdO3VpFIJguEALb9dSWz3DkxTR6xMvJnXI9IIHDwCmlQOHrOj7gwJcbQkz1fO16v+5qswy0uVOqyvpZHGB/0CXkpLdtShowesEdAIDEZAk8pgNPTn/SIgfCKpW/L6rdJT51B70fk4sZRK59L8wHJSyYH81/ttQ+/UCGgEjg4ENKkcHfM8eqP0RF6xmHrbYhw7iB206XtrFS1PP68LeI0eyroljcC4RUCTyriduiPXcUmJX73gEornnUA2k8Fzk7T9+tG9CVt8JzDtCnbkZkhfWSNw5BDQpHLksB+fV5bqXZ5HoLCI+uuvgoQLJYXseepVejduVGNSySbFxVgnmxyfc6x7rRE4BAQ0qRwCeEfjqR4Gpud7ek1avIhQTQ1WJkN/bzNtd/nuxShC0bfW0Xh/6DFrBPQvX98DB4WA5PqSIEdH8oHNmkXlgo/hxj2CIZuGh1eQ7NyDYVpkxfaii60cFLb6YI3AREBAk8pEmMURjcHBc11wRJ0lVhLYuu4Vnntz/Ye3Zu51BGPmp27GCJqEA0G6t22h+YlnlMFeqb50VvwPx1IfoRGYYAhoUplgEzrs4YgU4RlkTQ/PsMjGO/mjxdfx1W/9/EObMMW7WMWtQMVFZ1F69ik4iRQBXHbfs5Ssm/XjWvTd9aFY6gM0AhMNAf2zn2gzOtzxeKYqBewaEtoI9/ziX3l2YxtWXxPdB+G4ZQZtJt38SZKuSzASpful39HzymvYQjq61PBwZ0MfpxGYMAhoUpkwU3nwAxHtVBCDzh2/4x9+8FOsUITO3hbauxMH1dika6+kYOY0Em4WJ9FLw91LDup8fbBGQCMwcRDQpDJx5vKgRuIaLhnEluLy0x/eSahkCtUhk462DpqbeofdlpQTLqippG7RIhiIYxZGaXzyWeK7W4bdhj5QI6ARmDgIaFKZOHN5kCMxiJg2b/32fp7f6fKDH3wT20iQ6m6npblj2G25rquCHus/dQ0FhRUYloW7fTe7lz4x7Db0gRoBjcDEQUCTysSZy4MaiTK0Z/v57g9+zM1f+hqXnHUsVmEZWSfG1uaGYbdlGqZyHy4/5SQKLjkHpz+JHTZoum8Jbio17Hb0gRoBjcDEQECTysSYx2GNwpOgRDeLxLrL9vjPfkRf8Ul8duHpeFYBBaFiJHBx0/rt6nvPy+J5zgGLb0ncio2HaVhM+fT1CMk4kQixt96l7bmX/H5lPbJO1v+s/9UIaAQmNAKaVCb09O47OEmfIoQiRBDvWM8P/ncJX/2rvyAA2EXFzCoXsvHo3L3Fz+NleColy76tvO8vQ1rzt6kLLqV0zvG4SYdsJkXDXY+oL1zxQc4f9L7T9Z8aAY3AxEJAk8rEms8Dj8YUN+KAWt//+Sd3MmvhZ7nmjBnqHDMymWNn16vPrR076Uz52YjVwUIuQ2xCVEYuZkWIqfqGT+CmEgSKwvQ8+Rz9mzZiSLCkYQ3Rgt6tEdAITCQE7Ik0GD2WoREQWpA68rZh0bTpNe788Z2cuGAxX75jh5IqgpbBa++2UhyKsqOxjebOGFWTCpX6C8OXboZqfTCx1N9yNS3/dieJVILYnmaa7nmE47/9F3g54hmqDb1fI6ARmBgIaEllYszjMEchOqgUP/z2t7lg8ee5Yf6FTJs6hVnHHMPM4+ZwyvHHKhdjr7OJ9o72XJuqPNeQ7YuUkpdU5KDiY2ZRPv8yMrEkVjRE8yPLiff26wJeQyKov9AITCwEtKQyseZzyNGIBss2TF577Bc8tSHF06/+lOrwvoe/OSvEb554glQyRXNTF5w8E6W72vewIf+SRJOiLqu97ToaHnqCYMCga8M2Oh5fwbTbFg95nv5CI6ARmDgIaEll4szlgUciQkq6l3/4zp1c86df+wChyMnlFZOJRgpIpwbYsmWH355iigM3nf9WLiGvqksvovCMuaQSCQKuR+M99+YP0e8aAY3ABEdAk8qEnmDJQOwiNg/ZnrzrR2zJ1HPH7VcpL6/3D72iZiqTS6LgxNnZ6MeqGIYjye7ff+gQf3ukXYdgKMSMGz+BmwWzMED76+/Q+MzzZHtj+xTukm65roejIvuHaFLv1ghoBMYVAppUxtV0HWRnPRPXc5TNI9G1nb/4wf/jU398B1VB4RqRKfbdiisrmDW9Wu1sadyFRJYY4ro1zE0clg3PIwPU3HIjReJenE1jp5O8/Qdf5oXLruGFSxez9js/ZGD3biXWeI6ButAwr6EP0whoBMY2AtqmMrbn59B6Z0hQokSheHz3r+5gpzOJ3//DK4Zs04jUUDVpMrCOpk1r6c5ClT18UhGDvdxQkqgyYHhYBREc18EzXYydO+ncuZEsNh3PPcuu/32Quf/+PaZfMR9XiEVvGgGNwIRAYPgrxoQY7tE1CCebZPP61/jGn3yGf7jzMTzTZPVbb7GrYadyL86j4WYS7Ni+jRVPPsLTL7ypdm9a/Tr//OM7WbtxK/GkyB7D2Uwklb6TSPDGF75K36pVOJgU1R/L1C9/iRP/+jtMu/wazKISsts38vbtf0rnSy9jWPo2HA66+hiNwHhAwPDyCvfx0Fvdx4NCoLt5E392xxdY32IyY+oUkvFeuvvjnHLWeXz/298iEpBId4PuXW/xze/8kK0NnRRGCygsDRPrjNPb141Veyw//cH3OWFGDa4nks/QUoVIKEIPW3/5a97+w69iBWHyjYuZ86O/o7Cq0u+7B9v+927Wf+O7OO0tVF16KWctv49AKHRQY9MHHzoCmzdv5oILLqC7u5tf/OIXfOYznzn0RnULRz0CWv01gW+BktrZ/OL+Z9g30sRT5IBkF/Y8sl6Aoikn8R+/vAvjA1HvkhpfCgNLdi/fs+u9Dx8ETghFcnw13L0UhwzR087hpP/4B4JFpWSlFccja5kc83u3kmlqZ+Nff5eWN95mz+tvU3fh2R9sUO/RCGgExh0CWu8w7qZs+B0WI7ulygYLNfgp6vdKG6qMsIltZJUx/oOEIufkbw/Xz9ai/j3w9eMtrWS2bsHGpf7qKwgXleKlHeUw4BmmIhZpoe6GyzHqavFiffS/8+6BG9XfagQ0AuMGAS2pjJupOviOGhLxKDopcQo2xDFY8nSZKuuwYdiKMkzP8UWQvaLIe9fxqcTGGuxSPLT2S53oDiRwvCwWJpGKKuUJ5tkupvI2yyLFwaTepF1YRKAwKsEzeLHkexcdpU9yFc+VnGOQNVzlQGDsJcnhX0QwczyUtJfFIfABaW54bYnbtPK4M6QXhurX8M7UR2kExhcC+UfR8dVr3dthImD4q6okdMRQC6NMuF8+3l/cMGyQhXI/ZCEpIP00kLkv93PM+zsSqarAjhSryJPed9arDMh4tsqM7BgurmOqpT2+vRWnrYMMNuHqmvc3c8h/S1ct32SEJb7RoskbwSYcKIQoAp/ljPznYmZNn1iFVBTRj6Az+hSNwDhAYOS/knEwON3Fjx6BQHk5hWeeRgaL5kcfpf31N5FklZZlgRnECti42Qwb/+1O4rF+wjWTKT/vlFHvqJBKNpPG6e/FEe8yc2S3umMaGG4Wr7tbsdRww0DfP6CsCa5lkG3twtGs8n549N8TCIGR/dImEAB6KKOHgNRqkUX32C/eTrSwlGxrM+/e9kW23vcw8a5usj39dK1ez6u3f56Ox5cSdFxqPnkVBcfNHrVOqB7kMgi0/e411v74TiWxDNbgHczF5AcysGEDa/7mBxhKdeefLdc5GIIxTYNMVzvvfOPvSfV17e3CQWTB2XuO/qARGMsIaFIZy7MzzvomVhsDl/LzzuGEb/8ZLhZ9W7fyzme+wu8uWMQrl36Cl6+4nub7H8aJp6j82HxO/Js/H6lm6oPouJB1pbqlv9y3PLiMnb/4DenuHt/X+YNn7HePeNnnPe1F4mlZ+SI7fnkXXRs2+1pC+V4y4AyTEaQ3okbc88Ir7LrrV/S8+La6ruOKlWa/GXP22y+9UyMwHhDQpDIeZmmc9FEWT8PxDdszvv5FzvrPn2KdcCJB18RobCSzdSPxzk6CJbUc+9nPcfr9PyNcWYkllvBR2DzDw/YssEzS7a20P72SVEMDHcuf35/JaFhXdJMJmh9+Ei/ZQ+uDj6tzXEn373qYYmgZxpY/qunuJ8h4fbTc/QBS1FkKl5ki8RygCNowmteHaATGFAKaVMbUdIzvzojp3zMsLM/3G6v//ZuZ//Ij9H3+Rn6TjvPbgMExf/lnnPfUfcz75T8TqKjCy8gj/wit6O+HS5Jn5ioXNz3yJL27GggHDHbcd7/yeHv/4UP9Pbg+TNsLr9K5ehWhUJTWhx4n2R1Tp2VF9MizxVANDdrfu2ETHS88T7CwmuZnX6R30ya/Do1k3TwoRdqgRvVHjcAYRECTyhiclPHaJbXGGh6uKREujspAHCktp+/0E/mfdCc/CyYpv+MzVJ52slqPxZ/dFBetg8gvdiBsVEiOCU42Q+NDj1OQtQmHiuh88Xd0v7lanSoJNiVWZ8jNExWaZGb2GWPHfUvIZpK4BRF6NmykdcVK5b1meCbZA5CKOHi5rqvckeVazQ88THpPJ4V2lFR7B233L1VdEKSMYUo8Q/ZZf6ERGEMIaFIZQ5MxEboiaVws5bxsKddlGZOVyqj4mCLPxuwbUMOU9VityabIN6N0G+YyKve8voqO197CLAyRCYZJ98bYffeSnDxgSHXkA2yeEhwkrCa2YxvdK54jGI1iGAEMz6Xxnof8dkQiOoBrsIxNLEzyf6q3j90PL8OIRFTMjBkN0PzQctJ9/XjiFXeA1DcH6Kj+SiMwJhEYpV/zmByb7tQYQiD/UH/A9fxQ++sJQUHDPY9gxGJkbZOM4VAQLmDP0hXE2xoxJfjzANdRQoMiOmi+/0mcpjaMgJ/pORCN0PP8q3StWq3IQgWODtGWIi5FsND826dIrt+JHQjimQZWMERi3TY6lj+tDPgH6s8QzevdGoExi4AmlTE7NbpjB42ASAWNLTQ++RRGNEAw4+FmsnjRIP27dyB2FtkOnGlfot1N0vEETQ88QToi6ikPJ53Bs22S/d3svPdhFaGPNTQdCDmZIvR4Hm13LyFNBsM08JJpv30jy857fOkpT7gHPV59gkZgDCKgSWUMToru0sgQkJu5eekKEjt3Ydo2ZkGESHU1ktrfC1q03LsML5PB+hB1k7TT/tyL9K9fjR0NYtk2BVOnqYj4cLCAxsefYKB9D/jUst/OCt2INq77nXfY8+JrBAsiBN000TkzMT2TUEGQ9t+9QPcb7/qZdJSbsrgqD01U+72Q3qkRGGMIaFIZYxOiuzNyBFwnw+6HHse0TczeNJUXX8Ccb30Na8DDCwfpfX0Nba+8dkALjkgNYioRG4ybcbHjWYqPO4GT/umvMQnihW2ymxppeWx5zpS///7m7TZN9z5GsrsH0/Uwqus46V++TaiyBsf1yHT20Xzf0lx//FQwIs3oTSMwnhHQpDKeZ0/3fR8Eul94je433iQYDpI2bSpvuIIpN99A8NhjQNRg8RgNd/leV/uc+L4/Ypu20vv001jRApLJDOWLLqN24eUUnjmPTDKBEbRoE4N9dmhXaBGGEp17aH1kheqPExug6OMXUX3BRZTPvwCnP0k4EqX18SdItXf6NhpDQkf1phEY3whoUhnf8zcuep+PPM+/j16n/cj3vMJo971LITGAm00TOm4GdZdejBUIUHftfLxYCrfEpmP5U8R2Naou+Oe5SjRxBkXR737gcVKtnbg42JOqmXrdQnX85FsW4WVTeNEQna++Teerr6v9kpVZ6tOIp3JGQu1zwZxNjz9L77bNEDTxCsLMuOlqdfy0W67FLiiWZM30bNtC8+O+rUeaeT9GruvgOn4oT+ZArtCq5eH98/5rDO8sfZRGYHgIaFIZHk76qFFAQIIKCwsLR6GlfBOGCiAUhVGyuZHmJ5/FioZw4lmmXb2AUHmZOnDKTVcRqqwi5EKspUkZ4OULRSoq3Yr6B4mUlySXzUsfx4gE8eL9VF52PkXHzkZCFCdffTkFs2YSTHk4iSS773p4r2QhmcAk95nEt4iRXiLm2x54HNN0ceNpyk8/larzzlL9KTvnDIrPPR0jlsS0bJrvXYLjpHEl5+b7fNM801L7JZF04ENsQXlUPuw9H9wpc5H//GHn6O81AsNFQNdTGS5S+rhDQkAWL3lCXrFiBbW1terzoS5osoiLXVvsEMEnnsJuaSVdZGCXV1J/83WqvyKBFJ18CuWXnM+ehx8nGAjS/PBSZn3xNpxoAQHJVmZ6qpiZqJ46VzxH/J21UGSTTUaYeeO1qh3LAbuihrprrmHzD39GcThI27JniTfsoLB+BhnDVd5ekuTfM6HzzVX/v70zf46qyuL49y3d/bqzmqWTTmcBNAZwAUYRBTQQ1hCSQIhCcH7xF7VqrJqZH2Yry5kf5j+Ymd+mSn9xVJQBLZHIOC4zoOO4oeK4IKIISZAA2Xp/y50696Wxg0qCSSeBPo9KNZ10n3vv51a/b99zzz1HHrr0+QoQi0VR07kVqseAsIUUkpqudnz48r/hywvg/Bvv4tzrb6P0rhVuin633oCUFysRx8k/P4b4wACiKxZh2DBkO5OZDJoHYt/T0yMPaE52HibTF37v1UeAReXqm9NZNyK6iamqCsuy8OCDD37HxfPjOyxgqwJ5NvAb7RosLTIQHR5GxcYmFCy6Qa4ihOPItPvzdrShb98BGIYX5z88jJ6XD6G6dSMEuasUSu9CcgCcfuJZ90R9UkfJwiWoaGp07ag2VGio7OrA1399HEnEkeo9idO79+O6X/5MRoZpFHpMaf4B9PztOaSi52VtmYKaagRHXWhCoX0YHVWt63H0+rlwTvQiYkZx6ql9CN61Ag5t1JObi/KLATj12C7899e/RbnmxX6Pgj9pMfjT/r4fD+6CqPt8Pjk37BKbBEx+6xgC7P4ag4OfTCWB9DdgSldimibi8Thsm9K3OFP2o5k2bAfISzkwzw7ATKkIdm2VRcnopqxrmrw5l69fi6KbroVpjUBN2ji1a6/8PVXHVMnvpAADH3+E3oMH4S3Ig0gkUbe1BRqdpqd0Moprp2zxjShqXAYxkoDmA75+phtWPHGhGBoJSqy/H/3dL0IJFMKORVC5uRn5VZWuHZW+xwn4y8oRalmHuBlBvt9A34svINpzWrrgLMtN72Imkvjy8adhGH5oxYXwKhRyTHs37l7SZDiSDXp/IpFAMpmUgj+Vc8+2cpcAr1Ryd+6zPvL0za+lpQUvvfSSXDGkhWYqGif3lyYU6XoqPXocI7u6UX/7EoQ71ku3WGZ0rl4QQGVHK44+8hH8gTyc+8chDH36CYrnL5CiJFcpTz0P89wgAnkGEKpCxY4Nspv0t/RFolG7swOD+16FE2gc+QAACQJJREFU6lMw9N4RnH71IKo3rXPTslCK++cOYOj418intCyBQlR1taXfLh9p/4XWITU7OvDVo09CiCTsr/pwavdzaPj5AxBUUEwBev/1BiKHP4YW8CIRc9D2yO+wcfmtUKdow546Q3NEQt/Q0CAfaUU5lXM0ZuD8JCcIsKjkxDTP3CDpBlVbWyt/stqLVU0w778POjS5qS4LlYzuTaTbrevchq/+8ijEcATm2TM49fQeFP/+YVlrJTF0Hj17D8DwepGMJhC6uxF5c+dJ11fmcp48T1Ub1+KzmxZg5PMj8Fg2TuzaK0WFNvpVU+Dkk3tBSe3NRBSFTatQctst6S7IRyEodFig9NbFKFm9HGee74bH0NDzzB5c/8B98kwNCVnvE7uhJGNwdAH1uoVY+YuHAL9vjK2pfEIrF76YwGQJZH5eJmuL388ExhDI+jde4UbvyluhA1lLhTbuKXvKxdWDHTgovG4OQmtWI5qMQgvo6N3TjdjQgNwDOdP9GoY+/x9EQIdmGJizvUOOhb7Jj7kcwFtQgKptzRAJG06RgcEXX8PQ0S/kIca+t99C/zvvwZPnQ1IRmHNPm3TBZdpQaZ1CYcIAarq2QNFUOIYPg+9/Kk/y04cyeuw4zv7zNaDQgBOzUd3ZApEFQUmvJumR5ivrc5YJgv9/VRJgUbkqp3X2DCqrNylFlo13T6STxyj9nL7mZ/qsaE/ETT6McFcHPLpPnl8Z+fgYzrx8UMLqe+p5QDEhYkkUL7kZJY0r6OgJ1AtBwy5Tiuyirfbabc3wlVXCb6lI9p9Fz9MvyCb7ntgNJxIBLBuFdXMQbm12LWRqEyUvVhSkIBBauwqFDddDTwogYeLYrr/Lhnqe7cZI/xl4HA2+khDCd2++eEhTMslpIUk/TolRNpLTBFhUcnr6c2nwdBMHylffgeDinyCZMKEJC33PvICRIx9g8PW3oPnzYaUEgp3t8Po8csVzsSjSwsUSAkXzF6BsTSMSkQR0w0Df/v0Y/uIT9L96CB6/D1Y0jurWZnjLSqWrK1MRSF+EQsWWBYzia1CzpR0x04Q/4MHQK//B8Pvvo3ffK9C9HiSjcZSuWYniBQtGD9bk0pzxWK9EAiwqV+KscZ8vmwDVR/FYgO7zo7KrHTABUejF4Jtv471f/RHJ1DBUS4GvJoRQxyZpn86vjMnvSK41x4Hq2HLfZt5Pt8A2vHD8HsSPH8WR+x9G8ptvKOQM+jWFCI1u0KsUtpxxKVRCWCV3nfvxC+1og6+sBHGPCXNkAB889AdEPzsGw+MFPDqqd7bKaLaLPXEZJvm/TGDWEGBRmTVTwR3JJgGqrpjeZ6nY2gJfbSX0lI7E8DAGDr0Lj8eDVDSB8Lp1KKoNy664LqGMjwi51FQVHo3CAYDg6jtRuvgGWIkYnJTA2TffgSJ0iFgc+XfejuLFt0hXmUKKlqEIFPklC5ONuuiK5tejoulO2CMpeZDz3OHDsKwIrGQCxQvno7JpleyPo9C5fr6YwOwmkPGJmd0d5d4xgUkRoDMe9CME8sMhVG/eCCuWgKIDutcnd/z9Rj5C934b/vs9WzMX9mqkvvh8qNjeBl+MNl9UKHk+Op8PCC+u7WyHpiky/JcKc4lxUqyE7t0KXQlAtwGqDEm7+E7cQbCzBXpePhxLyJT5k2LAb2YC00CARWUaIHMTM0+A3Fg2uZ1Gc2uFuzphF/qhppJyV9+MxFGwbBFKVi67rM6Gt22BOqcCeoISSQK2GYWvoR7B5rVycULtUqjx6KLke23THkvl6pUoXLJIrk4sxYGeVGCHggh3bpYb/Y4UxEtZ+V7T/EsmMO0EWFSmHTk3OBME6CCkXHnQikEAJUsXo/T2W2FH41A0CzYchDtb4dFplZAZqvXDvaUUkoXhKgRb1iIRj4BO55uxFIJt6+AvLQHVVKHkkuNJAUWZGUYeara3QCRMmQ7Gig2iam0jiuvrZXSbqinSNfbDveG/MIHZQYBFZXbMA/ciywRoraAp8oSIbEnTNdRt74BqUeLICPxzaxBub3HDf8dTgdG+yg13yl58zzZZZVJJJmEUB1G3001xT2qgj9apv9TwSHhIxqo618NXHYYVT8IMqKjb6SbFpO7Ink+wX5dqi//GBLJNgEUl24TZ/uwjoLjVHataNsBffy0SkSEEN22EP1wpE9hPuMOOKqPAylcuQ+ltSxGPDKB01XIU3+gms5yInXR4Ma2OAjXzUL5pA7TIAMpvXIpyylrMFxO4wgiwqFxhE8bdnRoC5JoyystQ2b5GplSp2eFu0FPI8PgOK7cPlFFYdwQ8qi7Dh8mFVrN9sxvZNTEPmnSN6Y4CR1jSzVW7ox2OoqJi2yZ4Av7RHaCpGTNbYQLTQYBzf00HZW5jlhEQUIQt093XtDbj7EdfoviWm2FCyBPs7hH98btMwkQb6JS/uKJpDcqbN6Os8Q4pBKoM/53Yx4vqwWhwX1u2fAmC7XcjtGGV64qbsMSN319+BROYDgKK+E5yo+lolttgAjNJQMhiWbaqIhUbhnmiB4GFDVCptAr9Uy8drZXueTpvljzPYjqIfXkSWn0dVQmGorp1U9KvnegjrZMSJ05BDZZB9xqgAzETk6aJtsCvYwLZJcCikl2+bH02EhBAiurIU2SWvGm7WYMpPxglntTolxO4pIfLoVUPFQtToCqKLCOs0bEVxU1fPwEzY15iyXWOAls47pkVivoa54zLGAP8hAnMMAEWlRmeAG5+BgiMZjemmF+NTruPRlUJUhXpbppYmJU880KrGykmAirsUVPkEPvW7uWNkDrnwNHcU/juyfuJ9efy2uFXM4HsEGBRyQ5XtsoEmAATyEkCHP2Vk9POg2YCTIAJZIcAi0p2uLJVJsAEmEBOEmBRyclp50EzASbABLJDgEUlO1zZKhNgAkwgJwmwqOTktPOgmQATYALZIcCikh2ubJUJMAEmkJMEWFRyctp50EyACTCB7BBgUckOV7bKBJgAE8hJAiwqOTntPGgmwASYQHYIsKhkhytbZQJMgAnkJAEWlZycdh40E2ACTCA7BFhUssOVrTIBJsAEcpIAi0pOTjsPmgkwASaQHQL/B0eIfYphGDpIAAAAAElFTkSuQmCC />
1.It increases.
2.It decreases.
3.It doesnt change."
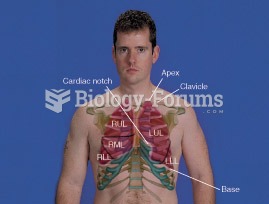 Lungs: RUL = Right Upper Lobe, RML = Right Middle Lobe, RLL = Right Lower Lobe, LUL = Left Upper Lob
Lungs: RUL = Right Upper Lobe, RML = Right Middle Lobe, RLL = Right Lower Lobe, LUL = Left Upper Lob
 Mobilize hand and wrist joints. Apply scissoring to knuckles and figure-8s to fingers. Holding the ...
Mobilize hand and wrist joints. Apply scissoring to knuckles and figure-8s to fingers. Holding the ...