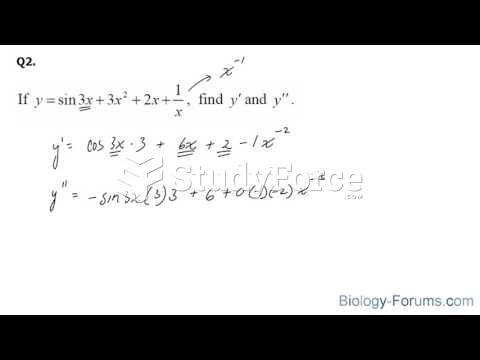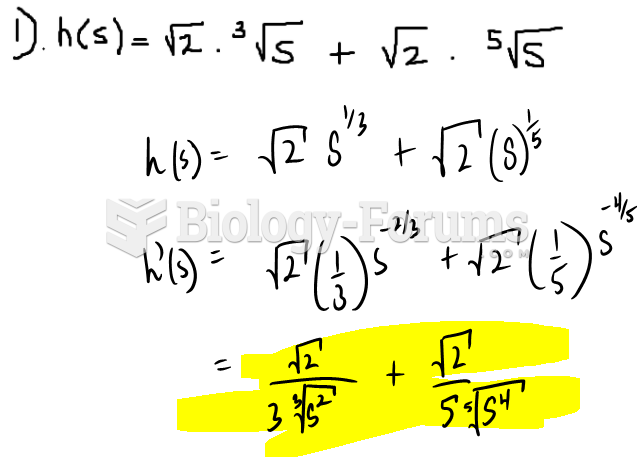|
|
|
Asthma occurs in one in 11 children and in one in 12 adults. African Americans and Latinos have a higher risk for developing asthma than other groups.
Urine turns bright yellow if larger than normal amounts of certain substances are consumed; one of these substances is asparagus.
The average person is easily confused by the terms pharmaceutics and pharmacology, thinking they are one and the same. Whereas pharmaceutics is the science of preparing and dispensing drugs (otherwise known as the science of pharmacy), pharmacology is the study of medications.
According to the CDC, approximately 31.7% of the U.S. population has high low-density lipoprotein (LDL) or "bad cholesterol" levels.
To maintain good kidney function, you should drink at least 3 quarts of water daily. Water dilutes urine and helps prevent concentrations of salts and minerals that can lead to kidney stone formation. Chronic dehydration is a major contributor to the development of kidney stones.