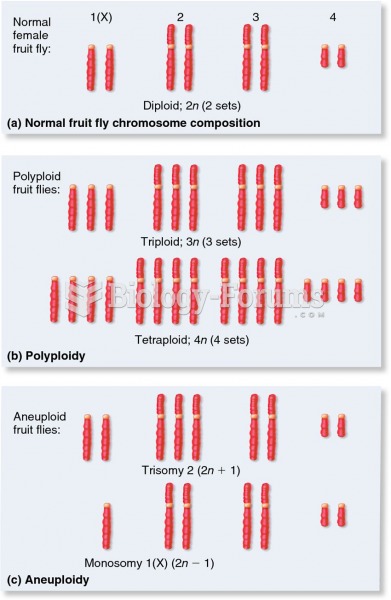
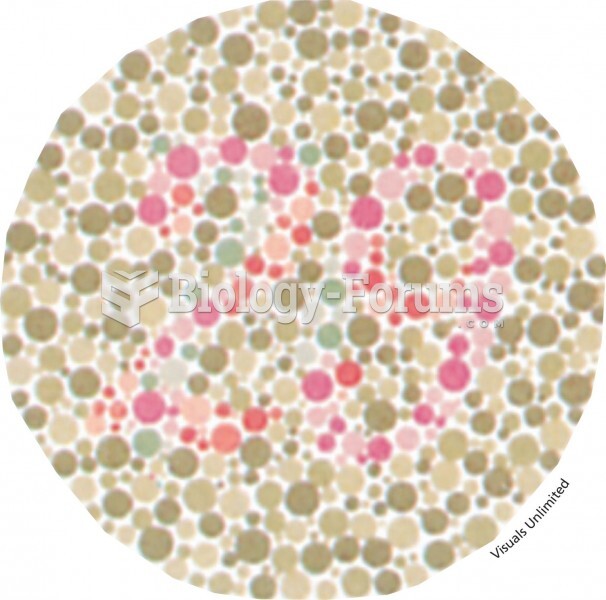
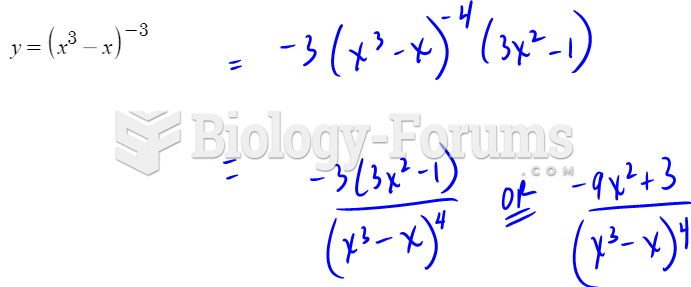|
|
|
Each year in the United States, there are approximately six million pregnancies. This means that at any one time, about 4% of women in the United States are pregnant.
The ratio of hydrogen atoms to oxygen in water (H2O) is 2:1.
Asthma is the most common chronic childhood disease in the world. Most children who develop asthma have symptoms before they are 5 years old.
Liver spots have nothing whatsoever to do with the liver. They are a type of freckles commonly seen in older adults who have been out in the sun without sufficient sunscreen.
The Food and Drug Administration has approved Risperdal, an adult antipsychotic drug, for the symptomatic treatment of irritability in children and adolescents with autism. The approval is the first for the use of a drug to treat behaviors associated with autism in children. These behaviors are included under the general heading of irritability and include aggression, deliberate self-injury, and temper tantrums.