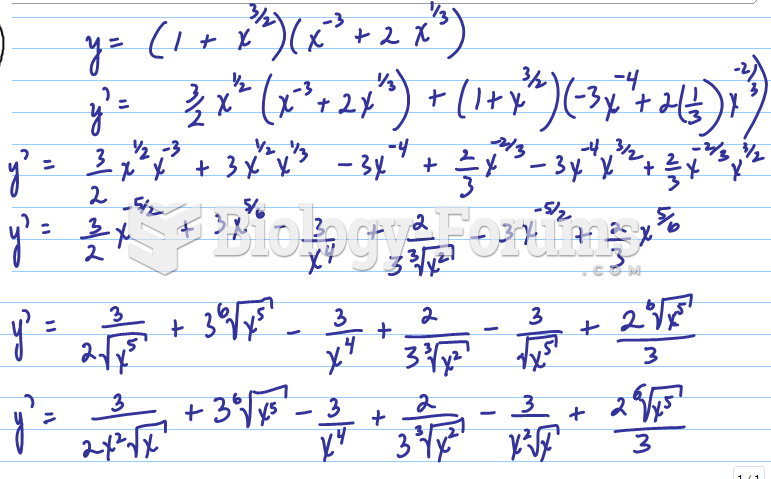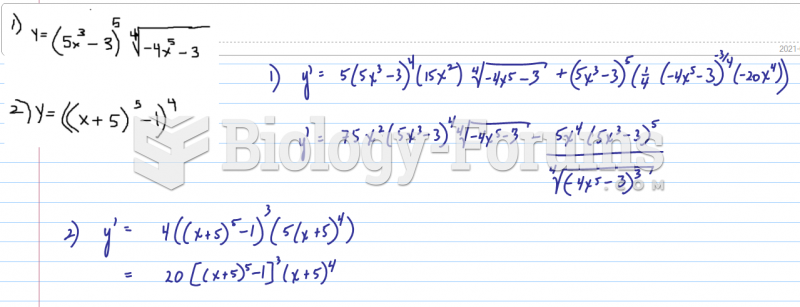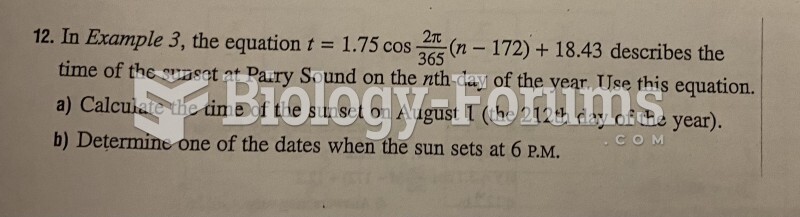|
|
|
Blood in the urine can be a sign of a kidney stone, glomerulonephritis, or other kidney problems.
A strange skin disease referred to as Morgellons has occurred in the southern United States and in California. Symptoms include slowly healing sores, joint pain, persistent fatigue, and a sensation of things crawling through the skin. Another symptom is strange-looking, threadlike extrusions coming out of the skin.
Earwax has antimicrobial properties that reduce the viability of bacteria and fungus in the human ear.
It is difficult to obtain enough calcium without consuming milk or other dairy foods.
In ancient Rome, many of the richer people in the population had lead-induced gout. The reason for this is unclear. Lead poisoning has also been linked to madness.