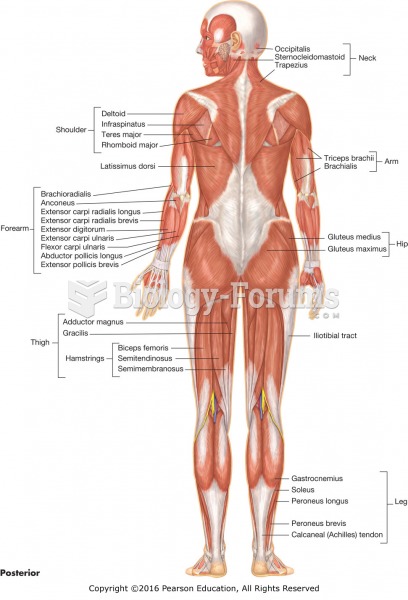
|
|
|
Interferon was scarce and expensive until 1980, when the interferon gene was inserted into bacteria using recombinant DNA technology, allowing for mass cultivation and purification from bacterial cultures.
In ancient Rome, many of the richer people in the population had lead-induced gout. The reason for this is unclear. Lead poisoning has also been linked to madness.
According to the American College of Allergy, Asthma & Immunology, more than 50 million Americans have some kind of food allergy. Food allergies affect between 4 and 6% of children, and 4% of adults, according to the CDC. The most common food allergies include shellfish, peanuts, walnuts, fish, eggs, milk, and soy.
Side effects from substance abuse include nausea, dehydration, reduced productivitiy, and dependence. Though these effects usually worsen over time, the constant need for the substance often overcomes rational thinking.
Drug-induced pharmacodynamic effects manifested in older adults include drug-induced renal toxicity, which can be a major factor when these adults are experiencing other kidney problems.