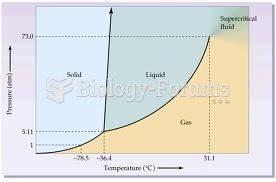
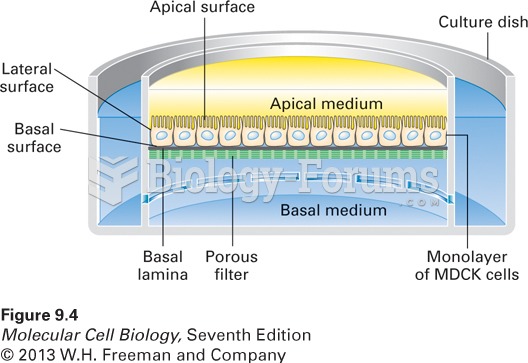
Provide an example of a phase-transfer catalyst other than the one used in this experiment.
Question 2Identify each of the following reactions as an oxidative addition or reductive elimination.


 Question 3
Question 3ByGsFEzhcExkpxh3Wqz88IkmApxqyAtMgpiNYgv8rlSewm+mykOjpfbD3BELFgzwAAABVy2fxjEOhAzxNnxvnJszxZKfaE9GskvCImT4zRhXow8PlooyIkMl8dZlskLGcVbeaKA2FGbdH5gCMRwpaFHijLjEmU80bOF/IRIiJUg7hRlx4bJfR8WZbIiR22E4hgJZ2OI36YLA2NkNphmrmg0L8yGw5bOBdcC5lOQGRcs88WSeKKk8FEOXJ5/gIwDxuUJ4uXcMLi6/GLkvqX5OdFye2wrLycoRlZn7KCoMHbUt7sALjBZHbBHWezQaPlc7/ILouNk3HAUhAMW8AdMIIYtDeSBLMDvGGgagP/JRgIBGwhBBuABa7lm1CNROiKA31hQBP6AiAdEY35+0lEeKIT6L2Na2dcapEtHC6Ue2eApxLm4Nu6Fe+Dh8OsDmz3uiruN+jGVR2clBhD9icHEQKLFGA8OZJ0DmxDw/40uDPY8mJ2Ei2A0h2/xCE8JXYRHhBuEHsIdkACeSKPIrWbwi4U/MGeCCNADowXKs0v7PjvcFLJ2wv1wT8gfcscZuDawxh1hJr64N8zNCWq/Zyge4/atlj/OJ2H9fT5yvZKlkpOcRdrYL8Mas/oxCuu7GnFhH/ajJbYMO4xdwE5jl7BWrAkwsZNYM9aOHZfgsZXwRLoSRmeLkXLLhnH4oza29bb9tp9/mJstn19SL1EBb3aBZDOw8vLnCPkZmQVMX3ga85ghAo7NBKa9rZ0LAJKzXXZ0vGFIz2yEcfmbrlgZgEkfR0ZGWr/pwk0AOFIKAOXpN515DdyuiwG4WM4RCwtlOslxDAiAApThrtACesAImMN87IEz8AA+IACEgigQB5LBdFjxTJALOc8C88BiUArKwWqwHmwG28BOUAv2g0OgCbSC0+A8uAI6wQ1wD66LPvASDIJ3YBhBEBJCQ+iIFqKPmCBWiD3iinghAUg4EoMkI6lIBiJAxMg8ZAlSjlQgm5EdSB3yK3IMOY1cQrqQO0gv0o/8hXxCMZSKqqO6qCk6EXVFfdEwNA6dhmagM9EitARdiW5Ea9B9aCN6Gr2C3kB70JfoEAYwRYyBGWDWmCvGwqKwFCwdE2ILsDKsEqvBGrAW+Dtfw3qwAewjTsTpOBO3hmszGI/HOfhMfAG+At+M1+KN+Fn8Gt6LD+JfCTSCDsGK4E4IISQRMgizCKWESsJuwlHCObhv+gjviEQig2hGdIH7MpmYRZxLXEHcQjxAPEXsIj4mDpFIJC2SFcmTFEVikwpIpaRNpH2kk6RuUh/pA1mRrE+2JweSU8gCcjG5kryXfILcTX5GHlZQUTBRcFeIUuAqzFFYpbBLoUXhqkKfwjBFlWJG8aTEUbIoiykbKQ2Uc5T7lDeKioqGim6KkxX5iosUNyoeVLyo2Kv4kapGtaSyqFOpYupK6h7qKeod6hsajWZK86Gl0ApoK2l1tDO0h7QPSnQlG6UQJa7SQqUqpUalbqVXygrKJsq+ytOVi5QrlQ8rX1UeUFFQMVVhqbBVFqhUqRxTuaUypEpXtVONUs1VXaG6V/WS6nM1kpqpWoAaV61EbafaGbXHdIxuRGfROfQl9F30c/Q+daK6mXqIepZ6ufp+9Q71QQ01DUeNBI3ZGlUaxzV6GBjDlBHCyGGsYhxi3GR8Gqc7znccb9zycQ3juse91xyv6aPJ0yzTPKB5Q/OTFlMrQCtba41Wk9YDbVzbUnuy9iztrdrntAfGq4/3GM8ZXzb+0Pi7OqiOpU6MzlydnTrtOkO6erpBuvm6m3TP6A7oMfR89LL01umd0OvXp+t76fP11+mf1H/B1GD6MnOYG5lnmYMGOgbBBmKDHQYdBsOGZobxhsWGBwwfGFGMXI3SjdYZtRkNGusbRxjPM643vmuiYOJqkmmyweSCyXtTM9NE06WmTabPzTTNQsyKzOrN7pvTzL3NZ5rXmF+3IFq4WmRbbLHotEQtnSwzLassr1qhVs5WfKstVl0TCBPcJggm1Ey4ZU219rUutK637rVh2ITbFNs02byaaDwxZeKaiRcmfrV1ss2x3WV7z07NLtSu2K7F7i97S3uOfZX9dQeaQ6DDQodmh9eOVo48x62Ot53oThFOS53anL44uzgLnRuc+12MXVJdql1uuaq7RruucL3oRnDzc1vo1ur20d3ZvcD9kPufHtYe2R57PZ5PMpvEm7Rr0mNPQ0+25w7PHi+mV6rXdq8ebwNvtneN9yMfIx+uz26fZ74Wvlm++3xf+dn6Cf2O+r1nubPms075Y/5B/mX+HQFqAfEBmwMeBhoGZgTWBw4GOQXNDToVTAgOC14TfCtEN4QTUhcyGOoSOj/0bBg1LDZsc9ijcMtwYXhLBBoRGrE24n6kSaQgsikKRIVErY16EG0WPTP6t8nEydGTqyY/jbGLmRdzIZYeOyN2b+y7OL+4VXH34s3jxfFtCcoJUxPqEt4n+idWJPYkTUyan3QlWTuZn9ycQkpJSNmdMjQlYMr6KX1TnaaWTr05zWza7GmXpmtPz5l+fIbyDPaMw6mE1MTUvamf2VHsGvZQWkhaddogh8XZwHnJ9eGu4/bzPHkVvGfpnukV6c8zPDPWZvRnemdWZg7wWfzN/NdZwVnbst5nR2XvyR7JScw5kEvOTc09JlATZAvO5unlzc7ryrfKL83vmek+c/3MQWGYcLcIEU0TNReow2tOu9hc/JO4t9CrsKrww6yEWYdnq84WzG6fYzln+ZxnRYFFv8zF53Lmts0zmLd4Xu983/k7FiAL0ha0LTRaWLKwb1HQotrFlMXZi38vti2uKH67JHFJS4luyaKSxz8F/VRfqlQqLL211GPptmX4Mv6yjuUOyzct/1rGLbtcblteWf55BWfF5Z/tft7488jK9JUdq5xXbV1NXC1YfXON95raCtWKoorHayPWNq5jritb93b9jPWXKh0rt22gbBBv6NkYvrF5k/Gm1Zs+b87cfKPKr+pAtU718ur3W7hburf6bG3YprutfNun7fztt3cE7WisMa2p3EncWbjz6a6EXRd+cf2lbrf27vLdX/YI9vTUxtSerXOpq9urs3dVPVovru/fN3Vf537//c0N1g07DjAOlB8EB8UHX/ya+uvNQ2GH2g67Hm44YnKk+ij9aFkj0jincbAps6mnObm561josbYWj5ajv9n8tqfVoLXquMbxVScoJ0pOjJwsOjl0Kv/UwOmM04/bZrTdO5N05vrZyWc7zoWdu3g+8PyZC74XTl70vNh6yf3Sscuul5uuOF9pbHdqP/q70+9HO5w7Gq+6XG3udOts6ZrUdaLbu/v0Nf9r56+HXL9yI/JG1834m7dvTb3Vc5t7+/mdnDuv7xbeHb636D7hftkDlQeVD3Ue1vzD4h8Hepx7jvf697Y/in107zHn8csnoief+0qe0p5WPtN/Vvfc/nlrf2B/54spL/pe5r8cHij9Q/WP6lfmr4786fNn+2DSYN9r4euRv1a80Xqz563j27ah6KGH73LfDb8v+6D1ofaj68cLnxI/PRue9Zn0eeMXiy8tX8O+3h/JHRnJZwvZ0qsABhuang7AX3sAoCUDQO+E9wcl2dtLKojsvShF4D9h2ftMKs4ANMBOcuVmnQLgIGxmENMWASC5esf5ANTBYazJRZTuYC+LRYUvGMKHkZE3ugCQWgD4IhwZGd4yMvJlFyR7B4BTM2VvPokQ4f1+u6MEdTNmLwI/yD8Bd0Rs573ioiIAAAAJcEhZcwAAFiUAABYlAUlSJPAAAAGcaVRYdFhNTDpjb20uYWRvYmUueG1wAAAAAAA8eDp4bXBtZXRhIHhtbG5zOng9ImFkb2JlOm5zOm1ldGEvIiB4OnhtcHRrPSJYTVAgQ29yZSA1LjQuMCI+CiAgIDxyZGY6UkRGIHhtbG5zOnJkZj0iaHR0cDovL3d3dy53My5vcmcvMTk5OS8wMi8yMi1yZGYtc3ludGF4LW5zIyI+CiAgICAgIDxyZGY6RGVzY3JpcHRpb24gcmRmOmFib3V0PSIiCiAgICAgICAgICAgIHhtbG5zOmV4aWY9Imh0dHA6Ly9ucy5hZG9iZS5jb20vZXhpZi8xLjAvI
Question 4j4KICAgICAgICAgPGV4aWY6UGl4ZWxYRGltZW5zaW9uPjMzMDwvZXhpZjpQaXhlbFhEaW1lbnNpb24+CiAgICAgICAgIDxleGlmOlBpeGVsWURpbWVuc2lvbj43MDwvZXhpZjpQaXhlbFlEaW1lbnNpb24+CiAgICAgIDwvcmRmOkRlc2NyaXB0aW9uPgogICA8L3JkZjpSREY+CjwveDp4bXBtZXRhPgoc0SEOAAAAHGlET1QAAAACAAAAAAAAACMAAAAoAAAAIwAAACMAAAYNU8Lu4gAABdlJREFUeAHsnVtMFUcYx9cg94uADa2iUrViK4i0BVsT++DBQhNBa4VqL/SCrReSmprUt/piI32wgDbSWAtvhBdqTU0r+FJMbKw0AuH2UHjh9sALlwAh3L/uN8mQsxwOw56zR/cc/5Ns5ux+s3N2fvN9/zMzO4Q1pCcNCQRAAARAwC2BNRBKt2xgAAEQAAFBAEIJRwABEAABBQEIpQIQzCAAAiAAoYQPgAAIgICCAIRSAQhmEAABEIBQwgdAAARAQEEAQqkABDMIgAAIQCjhAyAAAiCgIAChVACCGQRAAAQglPABEAABEFAQgFAqAMEMAiAAAhBK+AAIgAAIKAhAKBWAYAYBEAABCCV8AARAAAQUBCCUCkAwgwAIgACEEj4AAiAAAgoCEEoFIJhBAARAAEIJHwABEAABBQEIpQIQzCAAAiAAoYQPgAAIgICCAIRSAQhmEAABEIBQwgdAAARAQEWA/wuj2TQxMUFrg4NWddy+/ZvZ6v2ifF3dXfq48CPamLhBcAgLD6WMzNep5PsSmpycNLRBsrr24zXDdZyAgL8SeBIaYKcY82hEOTMzo50tPuNWg7v+69IeNT4S9nv19zSHI8ttWX8z6CKoFX5SqN2587sWFBSk7d//lpaUtEUbHh7R7t9v0HQH0tLT07U//7irJSQkiOYFh6wVeWlpmXbuq3P+1mQ8Lwi4EPClBtgyxqz+Revv76fETRvFKOv8+a+trv6p1/fBhydE2w7lHqKBgQHD84yMjFDe4TxhdzgO0MLCgrBjRGnAhJMAJ+CtBtgxxjQr+2x4eJhefS1dCMWx/GM0Pz9vZfWm6oqMiqC0PbtN3aMqzFMBFr1dKa8QTz2WS6Ojo/TChudFOS7PCUK5HClca21tpdnZ2YAC4a0G2DXGLBNK7nA5muK1uvHx8UUHcGQ56OQXRdTV1UX5Bfm0LjZGiAcL2fWK64vlrPzgC6GUv3QVP1Ws+KgP/3lILS0tGFGuSOnZNupLUyIG9GUZysnJpqtXy6m3t9evoVihAXaNMcuEsrj4rOj4rdtedJmS8oiKR1k8JU9J3UWfff4pZevOwU7Ctpu/3LTcQXwhlFuSNovn7ezsNPW8GFGawvVMFOZlmb1vZC7GQFR0JEVEhtOmzYlUdLKIqqurqa+vz69YWKEBdo0xS4SyrLxMCEhcfKwYSS3tXSkUl767ZDDV1taK+/bte9Nw3ZOTqqoqcj7CI8KIoTtf4+/zJsl2TE1NmapG3oe33qawBXzhjo4O4t0S0j9kzgMInnVxnpKaQhcvfksNDX+57KawEyCrNEAysFuMeS2Ut279SiGhwaLD5Zrc0g7kxsesi6bp6WmDic9Z0Ha+nGy47smJBLxS7u33yLrt1ome8MI99iDgyDrgIpTSz2QeGhZCcfFxIlYyMjPoyg9XqKmpifQ3z7ZohJUaINtstxjzSigfNz3WOzBWdPRKoyVu/J70tGU7lafI3goYV8zrgs4HT2N2JL9kuNbc3LzsM6z2Ii8bcFt4Ed5Mkp0vGfG67O60VFFXdEwU5byTQ21tbWaqtLysfEbkq9sfbBdOvNPiaSarNcCuMeaxUJrZAsBO5WuhXOosvlijPHX6SyFuqpc5pWWlYi1WvqiSQcVCWa4v2vMomvPu7m5q/LeRcvNyKX59nMva7tI2+fJcPiNyewolT8XZpzl/O/sglek+Vl9f50uXUNbtCw2wa4x5JJRmtwAEilA++PuBEMrknTvcbg/ibUPbtm8V5WpqaoSzSfFhoTx95hRduPCNwQnHxsZE+Rs/3zBcx0lgE+jp6RHiJ/3DOZfCuP65eDp+4jhVVlYSvym3y3YiX2mAXWPMI6GU24BYENrb24k73N0xNDQkROBJjygz92bQ0feOWh5pBe8XiPbwhnNus3MaHBykI+8eEXZ+ozk3NyfMMgDk1Nv5Hv7M024uE6h/7rm0vTgnscc4S982x+uP3PfyrTePGrMOOuhyyWVi0ZA+ZDdmvtQAO8bY/wAAAP//8fd5nQAABEpJREFU7d29T1NRGAbwhyBaxJJYWLAEHRo1/fKjVSaVSYwOUokSMVHEQFUcdNH4McEAEROLmqjAplRKTYhff4AYXRTxiqJuDGVgIgEaCG040sY2Ia1yCmLwnqcJoT3nvbd9f2/vQ2EBYhG3VTnZQvaroeF8vHbbdmfaZ8pbt1Zs2bo57d5KXAyHw+LgoYPxntYYVouysn2i9sxpUeGpEOuMefF1l3unGBkZSb78hFXbnbbkWuJOKBQSDqdd7C7dJSKRSGKZ33UuoGla8hoqP7BftLQ0i743fWJmZua/6Dzxnpb5nmkGrMRrLCs2FWR4a2xqlD7C7XLhcMVh2Gw2fBrQUo6bCxcUFxfj+7cfKXsrdSEajSIQCKDL34UPH95jbGwMBoMBDrsDx6qq4K33Ijc3N/nyE17l5eUo3V2aXB8YGMCRSg9MJhOeP3sBs9mc3OMd/QsMDg7CarUiOzv7v2s28Z6WeeGLyYCVdo0tKihlcFjzZwFfmw/Xrl2Fx+PBg/sPYTQa/3wAdylAgYwE/uY1xqDMiH7pxbGflGfPedHb24vWm7dQW1u79JPyDBSgQFJgOa4xBmWS99/caW5pRtPcny5aW2/BbrfPe1LzBjMsFsu8NT6gAAUyE1iOa4xBmdkMllxdUGjC+Ph42vNcaLiA27d9afe4SAEKyAksxzXGoJSzZxUFKKCwAINS4eGzdQpQQE6AQSnnxCoKUEBhAQalwsNn6xSggJwAg1LOiVUUoIDCAgxKhYfP1ilAATkBBqWcE6soQAGFBRiUCg+frVOAAnICDEo5J1ZRgAIKCzAoFR4+W6cABeQEGJRyTqyiAAUUFmBQKjx8tk4BCsgJMCjlnFhFAQooLMCgVHj4bJ0CFJATYFDKObGKAhRQWIBBqfDw2ToFKCAnwKCUc2IVBSigsACDUuHhs3UKUEBOgEEp58QqClBAYQEGpcLDZ+sUoICcAINSzolVFKCAwgIMSoWHz9YpQAE5AQblL6fYv5C9d+8uXve9xssXr5CTkyMnyCoKUED3AsoHZf/HfrS3P0QgEIDb7cbo6CgKCwrh9z9BUVGR7t8AbJACFFhYQMmgnJycRHd3Nzo62zE8PIyaUzWoq6uHxWJBJBLBlSuX0RPsiYfl3j17F1ZkBQUooGsBpYJS0zR0dLSjy98Fh90Br/csKisrYTAYUoYc+4R5vuEcrl+/gUsXLyErKyulhgsUoIAaAroPyqmpKQSDwfiv11++fsGJ6hPxgHQ6nQtOeGhoCMeqjsJqtaGzoxP5+fkLHsMCClBAfwK6DcpYyMU+PT56/AglJSXxcKw+Xg2j0Zh2itFoFNpnDa6drnn7ExMTqKuvw+e5vWDPU9hstnn7fEABCiggIHR0m56eFn6/X5SV7RNr83LFqZqT4u27t2J2dva3XYZCIdHY1Cg2bioR23dsE+FwOKU2dryvzSdMBevj508p4AIFKKBrgZ9tiSeZW446tgAAAABJRU5ErkJggg== />
 Question 5
Question 5Based on your background reading about the Wittig reaction, propose a synthesis of the phosphorane used in this experiment, starting with triphenylphosphine and whatever other commercially available reactants and reagents you choose.
Question 6The Horner-Wadsworth-Emmons reaction is a commonly used variant of the Wittig reaction. What feature of this reaction, shown below, is particularly useful compared with the Wittig reaction? Hint: Consider the structure of the product(s).
 Question 7
Question 7A researcher used column chromatography to separate two compounds. The desired compound, which was quite valuable, had an Rf approximately equal to 0.5. Two-mL fractions were collected, giving the TLC results shown below. Based on these results, explain what the researcher needs to do to maximize recovery of the desired compound, including the use of additional separations.