In this experiment you used R-carvone. Would the outcome of the reaction be different if you used S-carvone? Explain your answer.
Question 2Identify the product from the reaction shown below. The 1 H NMR data for the product is: (CDCl3) 0.65 (s, 3H), 1.28 (s, 3H), 1.632.55 (m, 6H), 4.42 (d, 1H), 4.82 (m, 1H), 5.00 (m, 1H) (Chapter 8). Note that hydroxyl hydrogens are sometimes not visible in 1 H NMR spectra (Section 8.1.4.b).
 Question 3
Question 3jkNS84IBB8BMxoDVylg7Nj61VaGX29wF9u3b5+gL5OLRo2BK87Busb0T8OGDZTvjnAZKfqqMdBjgVUZCxctVFtzG2lW4DIaXk+DpcFijYF+NCLznKcSInPcWOoQIeAPMdBEw9pyrDE3ejjD496SJUuCtp8BEwNtFHw74mWp2aVgqSN8Y2ClyRhp6Y/xDNX+E4EQA63HcPgEEgoyanQP1qhZQ2BzMqsDEwOrEQ19fTyVEGoVDbcXUQj4MpVg1DH5oiG5VTMNGTqYpMFcoiylSpWi6dNnUOVKlROlBRIRjVMJgeDhS1lMCZV4qjjJl7OjWKpUqQhjmSImBcWXjacX5bTQSy/VouLFi/uk6ndU6OXE36kEo2ql91Lq178fyT00HMmPPPIIxcbGUtasWalggYL0aPLkjjRvJ+nTp6PFi5bQo48+apiVpxIMYYmoSCYGETVcLGyoEQiUGGjyyq2gadKkiST3LyBpPa+iMXecKVMmiouLo4IFC1LKlKm07F6PyZM/SnNmz1UPd6PMTAyMUDEft279OurYsQPJFSWGhUAUkBabJZZq1a5FNarXpBo1aqgXrWEBHyOtJAZa09JNuiIIcltuRXpADBo1akRFivhm85ImTRrq2KGjW0LExEBDPHKPTAwid+xY8hAgYBUx0ES9evUq9R/Qn44d+5rkLpaUPn16ql2rNpWJj9eymDrCeKzd6+0ILyijEAxiIL0MGjWV5OPw9Y2XpXQqpAheyZLPULFixWjY0GF+YxMMYgCDWDnFRGfPniHUjzBVGsP26N7DbzmNCjIxMEIlsuKYGETWeLG0IUbAamKAr0zpjY/OnDmtiAG607VLV5oxY6alPWNiYCmcpipLLtXx0gbBkffPh/87d0SaPLGaGGik4Natn0juxArbMiUJEwOTA5LEsjExSGIDzt31DQEriYFGCn6UtgYnT50k6d9fCRMpxMA35CI7N5ZGli5TiqSHQbcdiYmJIZAB6SZbquOLUN269Si+TDxVqVKFsmfP7racmQQriYFGCu7LKYTBQ4bIZYR1HSIwMXBAwSd6BEJv78gtMgKRg0AgqxL0vcSyt3r164mKFZ8Vp06ddLIS79mzhz6rJee8KiEwGOvVr6s2aNJb80uSKODNEhs3FS9RTAwdOkRt7f3zzz8H1phBaStWJaBa7O0hbSBElSqV1TbsBw8ddLr3At1kzEB0wasSjFCJrDherhhZ48XShhgBK4iBnhRgUyBpW+D0cGZiEOJB9dLcIukDAIQARABLFnEO75V9+/UV2JhJGu95qSHwZCuIgSspgFRMDAIfm6RQAxODpDDK3Ee/EQiUGLiSAgjCxMDv4QhJQezACDIwYEB/sWnTRvHjjz+GpF19I4ESAyNSgPqZGOhR5nN3CLCNgX5ehc8ZARcEArEx0GwK7ty+Tbt27aaMGTOq2qVnRJJ+/x0tsY2BAwpbnMiHpduleKESMBAbA71Nwc6du9TKF03uQx8fomrVqmqXvCrBgQSf6BFgYqBHg88ZARcE/CUG7kgBqmdi4AIyXyZCwF9i4IkUoBEmBomg5ggDBJgYGIDCUYyAhoA/xMATKUC9TAw0dPnoDgF/iIE3UoC2mBi4Q5zj9QgwMdCjweeMgAsCvhIDb6QA1TMxcAGZLxMh4CsxMEMK0AgTg0RQc4QBAkwMDEDhKEZAQ8AXYmCGFKBeJgYaunx0h4AvxMAsKUBbTAzcIc7xTgi4s0rkeEaAERDC7KoE+XB2+CnAkkRPgVcleEKH04CAtipBOljyCsjatWsFVlLcu3fPa95QrEqQG1CJjRvf8SoLZ7AvArxc0b5jw5LZAAE4szlx4oRXSQ4fOSxefOlF4Y0UoKJQEIPq1auJ0aNHe5WbM9gTAbkTp0iXPq14Xr7wv/rqK69CmiEQqCSYxOCnn34Sb731pkidJpVYsXKFV5k5g30RYGJg37FhyWyAwOM5HhM5c+UQq1atEmYfvt7EDiYxuHHjhmjX/nWl6Rg3bqw3UTjdxghACzV5ymSRJTaz6NipgwBZCDQEgxjIKTQhdw0VsVmziLavtxHff/99oGJy+TAjwMQgzAPAzdsbAbkpjli6dKkAQahUqaI4cvRIwAIHgxjgJTJp8iSRMVMGUb9BfXH+/PmA5eQK7IHAzZs3RfsO7RRBAFHAWPsbrCQGf//9t9i+fZvyCglX39CacYgOBJgYRMc4ci+CjMDdu3fFwIEDRJq0qdUXOb7M/Q1WEgM8nLdseU8UKlxQPPV0CbFv315/xeJyNkfg6BdHFTktXKSQGnOMva/BKmJw8uRJUfPFmuKJ3LnE6tWrLdOm+dofzh8cBJgYBAdXrjVKEbh06ZLABkXYTMffrzeriAEezjVq1hBx2bKKefPnCblbY5Sizt3SEMB0Fl7EeCFj7M3Yv2hlcQyUGNy6dUt06fKWyJAxvRg2bGhI9o3Qy8/noUGAiUFocOZWogwBbKZT8pmnRZGihZU61Zevt0CJwe3bt0XXrl1E2nRpRK9ePUUwdveLsuGKuu5gIyfs7ohNnvCixgvbTPCXGMCOYMbMGcqOoHmL5uLKlStmmuM8EYoAE4MIHTgWO/wI4At9wdsLRLbsceKlWi+J06dPmxLKX2Lw8OFDMXvObJE1LlbUrVdXnD171lR7nCl6Ebh8+bJo2qypemFjC2XcI56Cr8QAhHfHju3iyWJFRekypcSBgwc8Vc9pUYIAE4MoGUjuRvgQwBc7vtyxvMzMF7w/xAC2A1gfjt+ePbvD11lu2ZYIaBqsYsWfFLt373Iroy/E4NSpU2oJbvbHsolFixcJGOJySBoIMDFIGuPMvQwBAviCr1O3jsCDdOGihW4fpL4QgwsXLogGDRsoO4K58+Z6/SIMQTe5CZsiAA0WbE2gUcJ9aKRRMkMMMC2hTVX16dNb/PLLLzbtMYsVLASYGAQLWa43ySKwa9dOgS83d6pXM8QAjpL69++n5pB79uwh7ty5k2Tx5I77hgBsULp162pog+KJGGAaAtMR8EeAqapz58751jDnjhoEmBhEzVByR+yEgP4h26JlC3Ht2jWHeJ6IAdS1CQkJym9C7Tq1xZkzZxzl+IQR8AUBrFioXqO6soGBLQw0CkbEAHYEO3fuUGTW21SEL+1z3shFgIlB5I4dSx4BCGjLu+B4aOTIEeLBgwduXSLLDW5EfNkyoniJYh7niSOg2yyiTRDAS/+99zaLgoUKqFU0M+XKguQxjzp+gwcPEiCg8K5oxnjRJt1iMYKMAO+u6LSlFF8wAsFBQPocoN59etOlSxepX9/+1KNnd0dDbdu0pQf/ekD79++n4cNHUOc3OlNMTIwjnU8YgUARkN4SSS43pAkTxlP27NlJarDoseyP0e07t+n1tq/TqFGjKS4uLtBmuHyUIMDEIEoGkrthfwQkyadt27ZSv/79iATR1WtXKVu2bHT//n0COQApiI2NtX9HWMKIRUDuY0CDhwwiuSMjlS1bjhbMX0AlS5aM2P6w4MFBgIlBcHDlWhkBtwhIZzEk/RGQVONS6dKladnS5VSsWDG3+TmBEbAagaNHj1J8fDw98sgjVlfN9UUBAkwMomAQuQuRiYDcppayZs3KD+fIHD6WmhGIWgSYGETt0HLHGAFGgBFgBBgB3xFgYuA7ZlyCEWAEGAFGgBGIWgSYGETt0HLHGAFGgBFgBBgB3xFgYuA7ZlyCEWAEGAFGgBGIWgSYGETt0HLHGAFGgBFgBBgB3xFgYuA7ZlyCEWAEGAFGgBGIWgSYGETt0HLHGAFGgBFgBBgB3xFgYuA7ZlyCEWAEGAFGgBGIWgSYGETt0HLHGAFGgBFgBBgB3xFgYuA7ZlyCEWAEGAFGgBGIWgSYGETt0HLHGAFGgBFgBBgB3xFgYuA7ZlyCEWAEGAFGgBGIWgSYGETt0HLHGAFGgBFgBBgB3xFgYuA7ZlyCEWAEGAFGgBGIWgSYGETt0HLHGAFGgBFgBBgB3xFgYuA7ZlyCEWAEGAFGgBGIWgSYGETt0HLHGAFGgBFgBBgB3xH4f1doza9Yr8JJAAAAAElFTkSuQmCC />"
Question 4Write rational arrow-pushing mechanisms leading to three additional products that might have been formed in the reaction of -pinene oxide with aqueous sulfuric acid that are different from the product you isolated and the decomposition product you identified.
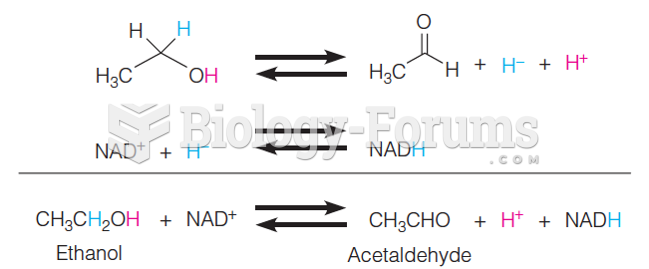
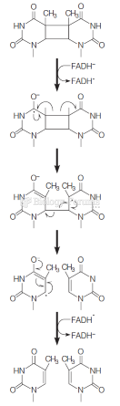
Question 5Write an arrow-pushing mechanism for the reaction shown in Equation E16.3.
Question 6Write arrow-pushing mechanisms for the reactions shown in Equations E16.1 and E16.2.
Question 78vej/fFVImVYEYFW7dtlT59emvzjIEDB0nJkiWz1Hv8+HHDE8eTMm/eYzLz3ply3XUdspxP1g+rV6+WosWKhp01T9Z1WA8JkAAJJJMABXMyaXqkrkwSzFOnTpGJkybK2WefLX1695FRo0ZLiRIlPDJSmdXMP//8U3LlzmmsfnwnBQsWzKzOW/QWwrdChQry8Ud7Lc6GPxROMKPEqVOn5DFDED9lCONs2bIZJhplJV++vLJv3z6BR47OnTrLkCFDpXDhwuEvkOCZHj27S+XKVWS08bvIRAJuIfDKK/+WX3/9TTp27OiWJrEdLiNAweyyAUlHczJJMO/cuVNq16mlsebIkUMgyjBzNnHCRLnooovSgZvXsEng999/lzx5c8tXR46mVLDZbI7j2SpWqiCYcT/5409y5pln2m5PJMEcXMmxY8cE9s0///yT4YaujJQqVSr4dMq+UzCnDC0rToDAuHF3y/Hvj8ujjzyWQC0s6mcCFMx+Ht0wffO7YP6///s/YwbtKXn88QWy+53dgo1RwemMM84QMQ5dceWVMnDgQOl+Y/e4XG4F18nviROgYM7KsHuPG2XFihWybdt2ueLyK7KeDPppzJjR+kE/ftwEbWZhVzAHVXHa17feelM++PBDGT5s+GnnEj1AwZwoQZZPBQEK5lRQ9VedFMz+Gk9bvfGzYP7ss89k4KCBcuDApzJ0yDC5Y+Ttmgn815511llaPENA//LLLwFWK1esTJm9ZuAi/BKVAAVzVkSI7texU0fp1auXPL5gYdaT//vp22+/FcxEYwb68KEvJE+ePJIMwYyZ53r160r//gNkzOgxlteO9yAFc7zkWC6VBCiYU0nXH3VTMPtjHGPqhV8F80cffSTNmjeVTh07yfTpMyR79uzSoGF9HRr4/PPP13axRQzbzHz58hkbAAsa//IbIYYLSN68eWPix8ypIUDBnJUrovjVqVNbr5LMmTNXBhjiFXbHZoLNcXsjsMkWI1z2uLvHyXhjYytSMgQz6kFglBo1r5Lly5ZL69ZtcCgpiYI5KRhZSZIJUDAnGagPq6Ng9uGgRuuSHwUzIprBb+xNvW6SCYZ9crCwiMaD591BgIL59HHAiknjJo20LTPMMlq3aSPnnXeefHbggKxYuUIww4zAJiuWr9AbW1FDsgQz6oIf6KHDhsiG9Rv1BkQcSzRRMCdKkOVTQYCCORVU/VUnBbO/xtNWb/wmmGGz3LBhA2NpuqJkgqs8W4PswUwUzNaDBndvEydOkGefe1bw3UwIQnLLLf20nTHMjcyUTMGMOiFwj351VN588y3R9v/mheL8pGCOExyLpZQABXNK8fqicgpmXwxjbJ3wm2BevHix4Tpugux5731twxkbDeZ2CwEK5sgjARMNeM34+eeftU/xCy64wHIlpWu3LlLo/EICM45kJET9g530ksVLpEWLaxKukoI5YYSsIAUEKJhTANVnVVIw+2xA7XTHT4IZs8uVq1wio+4cLb17947Y/Z27dsqiRQuNUMPrjE2BB3TeSpUqScMGDWWY4Q0AQSKYnCNAwewc+2hXnn3fbFm+fJns3LHLUqRHKx98noI5mAa/u4UABbNbRsK97aBgdu/YpKxlbhDMWDZG+uvP/wvbzw0bN0iTJo2lgSFo3zKWg60Swny3bdtGDh08LDlz5rTKIn/99ZcMHTpEFhhu5rB0XbduPbnIEMp//PmH4bJrm97cBC8a8+ctMEICd9F1mO1DGGGIBKbUE6BgTj3jeK/wxx9/SLnyZeWJRU9Is2bN461Gl6NgTggfC6eIAAVzisD6qFoKZh8Npt2u+EkwY+br448/imi73H9AP2NmeZEW3o8veNwI0lA6gAou5p555hm5ufdNetPU1i3bpFq1anrjFDJRMAdQpfxLLIIZ44Z/2NzJDZ4pHxp9ganTpuoXzJdfejmhC1IwJ4SPhVNEgII5RWB9VC0Fs48G025X/CSY4ae2dq1aMnz4CMvub922VerXryflypWTd3a/G3YWGsEfIL4RBRB+mTnDbIkzpQejCWZseHvkkYflecM/8ffffx/YgIaNaA0bNtQ+g2vWqJnSNmZy5T/88IOUKn2h7Nv7iRQvXjxuFBTMcaNjwRQSoGBOIVy/VG3M0jBlGIF7Jt+jjBlVR3t91tlnKvyLlNZvWK/zNGnaJGy2Vq1bKSOqX9jz6CeuM2/+vLB5cMJwz6XWrHlFf+Jns31XXnUFfmRKA4HffvtNc8dYhKb5C+YrwyRATZs+TR05ciTLaZRbvXqVuqrGlap3n5uVEZQmy3n+kDwCbdq2Uffdf19CFRoRDNX0GdMTqoOFSSDZBO6+e6waMLB/sqtlfT4iwBlmv7z5xNAPP80wIyIZgpLABtkqla9QTg4fPizv7/lALr74Yqsslsc4w2yJJaUHw80w33PPJNm0ebMsfmqxwDNEuPT3338L8q55dY288fqbRlCa/OGy8nicBLAK8+qrr8rbb70dZw3/uKmrXLmKjB41Ou46WJAEkk2AM8zJJuq/+iiY/TemUXvkJsG8ZPHTYdu7b99egd1kpE1/YQv/74QpfCNtLrSqwyxHG2YrOqk5ZiWYn3zySVny9BJ5dc2rOnKjnSvPmj1Ldu3apYN52MnPPPYJfPzxx3L5FdXl5I8/yTnnnGO/YFBOmmQEweBX1xCgYHbNULi2IRTMrh2a1DUsFYIZEcdKlCwucw3fr3369A1EHQvXC1OQhjsffNwUzOvWrTWi+P0T/jf4vNX3G7t3l35GUAfzOhTMVpTcdSxUMMNm+epaNWXzpi1SpEiR0xqLsbUaV8w0G6Y6MmTwYGnVqvVp5XggfgLwBZ0vf149JpdeemlcFVEwx4WNhVJMgII5xYB9UD0Fsw8GMdYupEIwG3ajkr9APt0UiJu7x94tvYww1eFMJUwhu379hrDN37NnjwwZMjgww/zNN9/I2rVrw+YPPnH55ZcLfCxfdHElQXjhT/btl7JlywZnifjdbB9nmCNiSurJUMGM1QWksXeNtbxOOMGMzNu2b5Mxo0cb98s6y7I8GD+BGjWvkjtuHymdOnWKqxIK5riwsVCKCVAwpxiwD6qnYPbBIMbahWQKZsOeX3bs3CHbt2+XKVMmy4kTJ3Rzzs1xruTMlVOmT58hPbr30P6Pg9tpClKrGUIznx0/zGbecJ/GJjBZsmSJdjvXo0ePcNn08Q7Xd5Ciho3shAkTpXiJYvoYBXNEZEk9GSqYIcxWLF8pCAFtlSIJZuSvWq2K4b/7bcvZaav6eMweAXimqVmzpiGa77BXICQXBXMIEP7oCgIUzK4YBlc3goLZ1cOTmsYlQzAjwt6/HvyXLFgwX2COUanSRfLuu+9o37jBrc6ePbsULFjQENNT5cZuNwaEc7oE89tvvyXXtLxG+1PetnW7nHnmmcHNC3x//fXXxPAAIMWKFZNP9x+QXLn/CYJCwRxAlPIvwYIZGznLlC0thw99Efa60QRzn769pVPHTkkJ5xy2ERl4Aqs+OXLkkJkzZ8XVewrmuLCxUIoJUDCnGLAPqqdg9sEgxtqFRAXzf/7ztgwdNlRfduxdd0vjxo0DM7K5cuUS2JAiIaAEbB4RJcxM5oxyugQzrgt71jfffEO6G3bNcx6cK3ny5DGboz8xQ96+/bVy7NgxmffYfB1i22wfBXMWVCn9IVgwFyhQ4B9zmgOfB65pjkngQJgv5j02atSdcsUVV8ZtOhCm+ow/DGHx3bHv9O9KPDAomOOhxjKpJkDBnGrC3q+fgtn7YxhzD+IVzDC/mDBhvNz/wP0ydeo0GTRwUGBz32PzHpNcOXMF2nL++ecF7Jfz5cuv8+XOnTsQZc8UP6a4CRQM+pIMkwxUhyAXLVtdY8yAv6uX59u2bStVq1aTX3/9VXbu3CkvvfSiYMZ85B0jZdq06boFZvsomIMGJMVfgwUzViXgEhAhz8MljFGk+6fvLX2kc6fOCYdyDnf9TD1u+KuV498fl8cenRcXAgrmuLCxUIoJUDCnGLAfqveRT2l2xSaBeAOXGJuwlOEJQ23ZusXmlcJnMwODhM+hlJ3AJZHKB58zZrnVjHtnqCpVKytDaAUCk5yTI7syIgGqF154Pjh74DwDl2TBktIfQgOXGBs21cmTJ8NeM1rgm5o1a6hDhw6FLc8T8RG47bZb1Z13joyvsFGKgUviRudIQWOVUK1atUohaM35hc7Tfxvx2f669uqtt97M0ibz77oX/24ycEmWoeQPFgQ4w+yHt54Y+xDPDPOKFSukX/9bZNPGzcbsbNUYr3h69q7duuiDy55ZfvrJ/x3Zu3ev3DN5khFw5BIZP2582HyxnjBEmHz11Ve6WOnSpS3DZZvtK12qtN64GOs1mD92AsEzzIULF5bBg2+TGkao63CbNSPNMMOjSpOmjeWjDz+OvSEsEZFAz1499J6FcN5LIhY2TnKGORoh95xHOPSu3boKzPCKFi0qTZo0kQL5C8jBQ4fkjTdelz///FNG3TlK71FBq/E7ieTFlTnOMOuh4/8iEKBgjgDHr6diFcwQl9UuraptFm+44Qa/YmG/HCYQKpjff/99MUKby84du+SMM844rXWRBPOYMaOliOHxZNjQYaeVy9QDBw8e1CZIJ386KdmM/8qUKS1XX11LsO8gltS6TWtp166d9O/XP5ZigbwUzAEUrv5iTLAJxhr7P+4ceaf2HoRN3GY6cOCAsaG6hY6k+tyzz0nbtu0omE04/PQlAQpmXw5r5E7FKpjhRip//nyyYP7jkSvmWRJIgECoYEZV/Qf0k+LFisv48acHrAknmHft3iU9e/aQd3a/q705JNAkXxR91QgVPm3aNDn1yympW6euFDJm75WxMffTA5/Kpk2bpGXLlobf9HFSvHhxW/2Fbfnzz70Q90oTBbMtzI5n+ve/X5brOlwn119/gyxfZr0SiJnnFte0kJrGStCmTZspmB0fNTYgpQQszDR4yMcEDA8Wqk2b1uqSyhcr2PVGS8aslMqZ61x15MiRaFl5ngQSIhBqw4zKTp06pWrVulrNvm+2rbqNjZ3q4ksuUrt377aV38+Z/vrrL2WYUal69eoqwxOMZVfxN8DYsKvKlS+rVq9eZZkn+KCxgVadmzOHrb8dweWCv9OGOZiGe7937tJZ2ytv37E9bCPxPDFmoJVhuqHz0IY5LCqe8AEBzjCn9HXEXZXDJnjE7SNk48aNxszbOdpjxP333R/RT+348ePks88/k6VPP+OuzrA1viNgNcOMTv7888/S7cZu2tPKDCMQTsWKFU/rO/I88ugj8uSTT8jixUvkqiuvOi1PJh2Aa0cwu8CIunn//Q9YmrQE8/jyyy+NmcLmMmXyFOnQ4frgU1m+L126VB41OGM2MZ4EN5OlSl8oxYoWM4Id7dCuJ+Oph2VST+DCUiUFNswnfvgx4A0p2lVpwxyNEM97moAPRD+7EIWAEX1PjRgxXM8M3dKvrzI2RClDnGivEXnz5VHtrm2n9u/fb1kLvEoYG/4sz/EgCSSLwBdffKEM0x89o4UZyK+//jpL1ZjJeuaZZ9Sll1VTV19dUw0bNlTdd/99asrUKXq3ftlyZbTnhh9//DFLuUz9AR5hut3Y1bL74byLYAwqVqqgDh8+bFkOBzFGo0ePCns+0olNmzepq2pcqfA3B6tWmPk2zGciFeE5BwngPoGnmliSV2eYDRejygiUpEpeWFI/G2PpM/NmDgFEZmPyKQHDt7BasGCBuqBokbAPJ2NDn+p1U0/9AMOD8KeffgrQMGbttIBBHiYSSAUBPKgMm3qVJ29uZYQmV8bOe9WyVUuVv0A+bYZhZTZkrJSoZcuWqQf+9YAyok2qrdu2KpgfMP1D4Pjx4wovEOFc8oUTzCj9xBNPqJtu7vVPRf/7P16wH3r4If23AWL3vffey3I+2g/G7LV2JVe4SCFlrAIow/e5du04cdJEVfC8Agov8Ua00GjV8HyaCRizxarSRRVjuqrXBDNexJ977lltkgRXeTA3Qp9ffvklw8z/75j6zsz+J0DB7NMx3rhpo4IvzJIXllDGMmrUX36IDszcFS9RTD311FMKvjeNXdAq+zln6+8+xcRuOUQAD6Nnn12thV3ValWy+HPFOTywMNsJe+Q1a15xqJXevOy9M+9VhilV2MZHEsx4ya5QsbzCqpSZUBfK3DlqpJ4hNo9H+4RNOny3FyiYXxkuAhWEPBLGF+MK22msJBghzNV55xdURkCkhGyjo7WH52MjgDGCgDRcx9ku6CXBbHjhUU2bNdX33tyH5qrvvvtOTxyNnzBe37N4ccfLORMJmAQomE0SPvnEbM6N3bvpX3w4Yscssd0EkYwZpmLFi+qNVkufWarfvO2WZz4SsEMAD6omTZsEHlTPPvusMnbkn1YUZkMQf/ny59VBEz755JPT8vDA6QSat2iusPkxXIokmFEGM75G9EtdHH8TDFtWLZhhRnH77SPUZ599Fq5qfRyC+Pnnn1OGNw09zhjv0DRx4gTVuEnjwGFsSqxTp7bejPzaa68GjvOLcwR697lZj7sRcTViIwzXj+qaltfo+yKcYEawG5j24d5wOmHjKl7g8DIwaNBAdezYsUCTYJ6IVSusquD3AHlwzwe/QAYy80vGEaBg9smQY2kb9pzm0nakh9rTTz+tmjVvFvahiqVcRPLCHwsjSIE6evSoTyixG04SsHpQQRTjIVuo8Plhm4b7D2YCuB9xX4YzNQhbQYadgDmGlSmLiSGaYIapi+mVxHAbpnLlzqnHyBRD+Axn5/zhhx/qvy1oA1YQwgmkjz76SNcZbKsOcY6/TVgVg3D59NNPzSbz0wECiOKHsUZEv3AJq5A5zj1HT7KYv8soExrpD6aB+B1v1KhhzCY94a4d63GYbcEkyGyH1UvlkiVLVO3atQJV79y1U9WtW0ebNaIPWIFhylwCFMweH3s8kEwbrNCl7XBdMzf8YanU8HMb1n4QM3oIh4oZvpmzZnIzRDigPB6RQKQH1YLHF+iHsp2NZNu2b9MrH0WLXaAWLVpEU6Ew1A0vFFnOBAvdSN/NQtgwCJtlpK5du2QJJY9ZZswOhwphuBUbOnSIXsrGizte4KOly6pfqh5+5OHTsmFVbOzYu7Qde+i+itMy80DKCGCMjcAl+vdz5Mg7FExsghNeaGC2gXvKvF/M+ytUMKMcTHIw0wyBHTqzG1xvKr6vW7dW4X4rXaaUWrly5Wn3r3lNbBrGPf7555+bh3RemDXiRQ79grkjU2YSoGD28LgH22DNmTsnJlszdNvc8IeNN/A4EG5WCjak+MPIzRAevlkcanqkBxVmirHRBpuLYD5kJ2EWEjb2sLWHzT1s75myEsBDPdKqEERNpISxAGPM/mJWH/kxRufkyK6Wr1iepShm3GCLXOSCwtoUDJ427KZp06ephg0bhM2O2UsjcEaWfRVhM/NESgjArrdmzRr6HsCLqhF0Rg0fPky1bddWC0vcGzBZMFMkwWzm2bNnjzbHgd06bIdTuWH30KFDqlPnTip3nlxqkrHJ9JdffjGbEfYT9xxMwUITXuTwuwFBDbNHmD8yZRYBCmYPjre5tI039YEDB+jNCol0w9zwBxdC4XYHQ0xjmRbeC7gZIhHamVHWzoMKs4d4kEGI2RXMJj2IbZTHwwteXujJxSSj9CY6K5twM0c0wYxVJdgUTzG8l8AcA6IZy9ibt2w2q9Cf6zesV5dfUT3uWTcIYrQlWlAkBMaAe0sslUcKopGlcfwhaQSw6Q8TMvXr19MrCBgzvOjiPjFt3c2LdenaWeFftBUjzF4jUA5cucFVJEx/kpkgjCcYm/dw/yIAC/4e2U1wX3nFlZeHzQ5zR3j0gfmj3dWUsJXxhKcIUDB7aLiCl7YxM2NlgxVvd4I3/GEDB2wMrZK5qx0PUcws0O+tFaXMPWb3QWXuSMfDNx7BbBKG/3DYu8LdGUwJYG6U6QkmWvBlHS5FEsz4/UbUP/w9gMkW8tYwZhixCcpMsF+GKIK7ygULErPrxCrBg3MeNKsO+wnRhnwQathkFmkGPWwlPOE6AjDduWfyPfrF+YaON6iDBw8m1EYI8eXLlyuYJVW//DKFFa5YE1yrQmhH85ABG2+YQeL3Bb9zoWZKsV6X+d1PgILZ/WOkW4hffPwBgA1WKncbY+Zu1Kg79R8w2CRiNtsqmbva8dB8/PHHuRnCClIGHYv1QdWrV8/Acn8igtlEDM8KCPcOV3SY9crkhxfEZbVLq4bdXBVJMGPFCu7d8DuNfA0a1A8sY+NlaNI9k7SQRiCkZHgOwLUQwMRuwosW2ggzMu6rsEvN/fnMlzAIVcwMnzp1KuZGv/POO9rEB6shjz72aEKmHhDvuNejJXP2HeYlcFFn5REmWh087x0CFMwuHytzaRt/SLDZxo4NVjK6hA1/sFPDHx9szLGyMzN3tZcoWVz7Z0UkL6bMI4CVDqx42H1QYec5xBiEMmxj4es7VpMMK8owG4IAw8woVkk+/vhjq2wZcQwv2BDNwTPD0Tr+yiv/1psqIQKwiQt7FvA7jpePVav+WT5PNlfYgeIeiMX2Gf0w7zm0EeYnmfyCFG1cvXR+3fp12swHM8SYKbYzrniJGjCwv95MOGTI4LCTPLFwwMbAylUusXV91Gu+yMFMEi7rwk00xdIG5nUfAQpm942JbhFmeuO1wUpml159dY3e8IeHL2wJrZK5qx32pFgK5mYIK0r+Owb/pZjtg3lOLA8qLLvCRy/8fcOGEeIZXhGSlYJ9qGKDUjJmQpPVtnTW8+STT2rPAHZeHODODb/jocJVb9Bq3CilM/d42cKLTqwJYgqrbVh1a9W6VdQl9FjrZ35nCJgbSfECjnsDM8dWyTTTMWd3P/jgA6tscR3DDDdslGONamm+yKHtcGFnNdEUV4NYyBUEKJhdMQynNwK/cBAic2zY951eOrlHMHMHLxqYuYNPznD+UbGJp2GjBnpjYHJbwNrcRCB0GTLWBxVmLREUoFatq/XS6w03XK8gzJKddu3epZf74cFh/oL5GWk2hFDj2MwLM6vQfQkYR5xHEBls5A22C8YS+aBbB2nTh1TbhkNYBPu+jfU+wKobVt/w92mEsa8i2LdzrHUxv3sIYJYWL+Lm5vbgACOYvDHthxEkx85MdKw9g51+PC/ywS9y8dpRx9pW5k8PAQrm9HCO+SpY+sRDDKYY+MUNFygg5ooTKICZu7639NGeCfAAxix4aMKMNJaymPxJ4IUXX9AzL5jVi+dBBZGG5VPYGqfDswUeXqYPVfhR3RLi6cGfo5S1V1gBgokFbIXBALbeNWpepWdm8bfl7bffylrA+Am+1/E3KB1jhL8rMMvBykMiCeXhUg/3FpN/COCF3AxhfcfIO7SpIGZ/EXY91Dd0MnuNwDtYCYtXjJsvcniGdzRsonft2pXM5rEuBwhQMDsA3c4lr21/rbYdhgN1bEDQfiSNTQh2AgLYqT+RPGb0I/jlxLJvcIJgxps/kz8JPL30aT3jU7hIIb2xJpbIV3jpa3FNC72rPFIkylSQg2iErf2KED/CqbiWm+vE7D5edINnk63ai1lpeAFIV0I471mzZyV8OYQ1hssvJn8RgGiFJwrse6hStUpazP4geOF9J1FXhtiHVL9BPVWkSGF/DUoG9oaC2aWDbgpms3nwUwl/lbD5xAaceN96zfoS/cT1YfdYp07tLHZaFMyJknV3eUS5Mj214FMvORobdSIl2APCpAezltcb5heI+OVEwu8PNrYxRSeAQEXpFMwLFy7UATKityxyDghm3GNM/iSAVQ94cElXQoCS4MAs8V73hReePy1ceLx1sZxzBCiYnWMf8cqhghmZsYEAS6vwRdq4SeOU2H1GbJSNkxTMNiB5OAsEM17akIKXHIODA8DsAhs/IU4RChf2+BCr4YLipAsHBbN90ukWzLBXha0q9kEkkiiYE6Hn/rLpFswQujBjwspMIomCORF67ilLweyescjSEivBbGbADN2txoYcPGDw6dSMndme4E8K5mAa/vseLJjN3mHJEYIZZkOYdTbDKMNOFvbKWNJ0ekUEbaVgNkcs+me6BTNahAA02GCYSKJgToSe+8umWzDDRhrRbRHVMpFEwZwIPfeUpWB2z1hkaUkkwWxm1C6fjJlmzDhj5tkNLmwomM3R8eenlWA2ewrfv7Bfh60wzHXcIJLNtuGTgjmYRuTvTghmbM6MFJI4cov/OUvBbIeSd/OkWzCDVM9ePfRKWSLUKJgToeeeshTM7hmLLC2xI5hRAKJk9epVqmy5MloQwNbZyUTB7CT91F87kmDG1fHShihbMMNo1KhhUsO3J9o7Cmb7BJ0QzGZIYgRNijdRMMdLzhvlnBDMCIyDiLaJTEhRMHvj/orWSgrmaIQcOm9XMJvNg/eMeybfo5fF4VUD3jWcSBTMTlBP3zWjCWazJaYPVfgSR3CTYB+qZp50f/pRMMOHMfxNx+KtxA53JwQz2tWpcyftLsxOG63yUDBbUfHPMScE8++//679kYcL3GWHLgWzHUruz0PB7NIxilUwm92A666u3bpo/83jx4/TgSHMc+n4pGBOB+V/roFgHAgf++OPP6btonYFs9mgYB+qc+bOUdgQ6FTym2CG9xFEScQ/uL9qb7iihCnMwQT9GWN8nBLM8H17WfVL475FKJjjRueJgk4IZoC5ufdNOgZBvJAomOMl565yFMzuGo9Aa+IVzGYFGzZu0PaAF5YqqZ555pm02ZNSMJsjkNpPmOKYYgm+SatdWk3hBQmuwFLpqztWwQwKaCuEEMyGYOOcTndlwaPgN8GMvi1eslhv/jXvBQR0wHfs7O/X/xa1ePHiuHzWOiWYce/C/aCdcN7BY2t+z1TBDG6JmAyY/Nz+6ZRgxnMNIbgR9TaeRMEcDzX3laFgdt+Y6BYlKphRCZZpMQuJ0MD169dTu3fvTnlvKZhTjjhwgR2G9wl4pDDFEswf8A/eU+B2cO5Dc8OGMQ9UEuOXeASzeQk81KdMnaIjBSK4RLqDl/hRMONlpKoRyMG8B4I/cW/kzZtHn6t0UUV1991j1dq1/9HuAM0xCffplGBGe3r07K4mGUGa4kmZKpjhoQZjf63haWTJkiVxvSTFwzvdZZwSzBDK2FwPe+Z4EgVzPNTcV4aC2X1joluUDMFsdu2HH35Qw4cP02IKs07ffvuteSrpnxTMSUcascLrOrTX4xoslMzvmG2EaILXihu736hDRMO2OJGUiGA2r/vFF18Y7emmQ6xDxCEKXzqSHwUzuGGTpSmYzLG3+kSI3py5ztX3S4OG9dVcw0QGM7lWM5NOCmaIknijhWaqYF60aGHgpQn3AkKNw1/6rYYfdPhDd5Pr0UR+150SzGjzLf366pe5eNpPwRwPNfeVyYYmCZPrCLS/rr00b95cBg0clLS2GQ9HGXH7CNm4cYNUKF9BOlx/fVx1N23aVGrXqm1Z9rXXXpU7R90p7+/5wPI8DyaXgDFjKK1atxJjNSFqxbly5RJjllfKG2OPe6txo0bSsGEjyZs3b9SyZoZNmzdJz5495PPPDpqH4v5EXcaLnBgvcDJj+r3StWtXyZYtW9z1RSto2MbKtKnTpFWr1lmyGi8VWX7OxB/++jPr/XNJ5Ytl7py50qRJ07TjMGzyxfBKIGNGj5EJEybGdP0H5zxo/H3bKKtXrY6pnB8yN2/RTNauXZulK2eccYbkyJFD/96XKVNGrruug7Rq2VJqGX+/s2fPniWvF35o2aql3HD9DdKnT5+0N9fY9CcdO3WUo199LTlz5ozp+i+++IIYq2uyc8eumMoxs7sIUDC7azwCrUmFYEblO3fukHr160munLkE14gnderYSVq0uMayqNcEM8WSSKhYshzY/x1MpmBGlUYELXniiSfk7nFjpWKFitKzV0+pW6depCaEPZcnTx4pXrx42POZLpjxMgKRZCwvS5UqVaRZ02ZSv359qVOnrhQoUCALNycEM+ZunnvuWRk5cqR8eeRLOeuss6RDhw5y74yZUqJEiSztC/dDJgvmLVu3SLNmTcXYWBsOjx5/cMa9UKNGDWnXtp20bNlKKlWqlNKX1bANivGEk4LZWAkTw12mfulY9syymFpOwRwTLvdmxgwzk/sIJNMkw+zdzl079caFNm1b612/5vFkfnrNJMNq6dqPx2DXjKVamGjAC8G06dMUNobG6mEjGSYZVvfbiRMnVIsWzfWyMkwH0NZY/0ULeuFHkwzsU7jo4kqB5fjQe9fcBFi+fDk1cuQdCn7a4e84Wkq3Scb777+vmjRtou1EYT5WrnxZHSYbtu7wADJ9xnQF917RUiImGaHsMuFnmOgE9zMaX6fPO2GSYcY6KFO2jP77ifvx+huujymMO00ynL5zknN92jAnh2PSa0m2YMaGP2xaMGZgtL9muMlJRfKaYE4Fg3TViT/kzZo3y/LAMx9+wQK5+uWXqdFjRusNK26wYbbigyhv8I6A9qfKxt6Pghm/z+aY4xMCGfarFStWUAMG9Nf2q7G+FGF80iWYg/11Dxo0UPvrHjp0iLr99hGB2+SNN15Xxoy3qlipQtRNVxTM/7gZDL4nwn3HCykEM16isVkYzxy3p3QL5nfffVc1btxIe/iZOGmC/v06evSoGjFiuH6RGzXqTnXy5Mmo2CiYoyLyRAYKZpcOUzIF8zvvvKPF8gP/ekD3FgFOKJhdOvAxNGv16tUBsQTXcpiZxcOxarWqavyE8WrNmlcUNnwmM6VihnnZsmVaLONlC+2nYLY3YnhQm2IIGzv79O2j/XJjtj7RlGrBjJnxx+Y9pgoXKaQaNmwQiAiJl8BSpS/Uqx/BfYCXgtn3zdb3SZu2bdT+/fuDTwe+JyKYA5V49MtTi58K/A0w74vgT9ODTu48uVXLlteoOcbLFlYdDbMoz/Q4XYL5u+++UwMG9tf3G56X8PAzePBtOrCOCQsbZtGeosUuUAsWLIgYPIiC2aTm7U8KZpeOX7IE83vvvafDFN93/32BnlIwB1B49guEhfkwhEeBQbcOUi+//FLSBXIooGQL5hUrVuiZGkTR+u233yiYQ4FH+Rmzr1999VWUXLGfTqVgDvYRj8A7uJfNtGPnDh2GGILaKmF2r9dNPfXM6Bhj1STUw0qmCma8JCF8s/k3AZ9YZTK9ojRq3FA98MD9auu2rZZeUaxYu/FYqgUzXswwsVTwvAKqS9fOCoHAkHCPIqYBXu6DE46/9NKLevXj8iuqq3Xr1gafDnynYA6g8PQXCmaXDl8yBPOePXv0DM6s2bOy9JKCOQsOz/6AKHqYCUlnSqZgXrVqlRbLr7/+mu4CBXM6RzLytVIhmOFOsNuNXSNGIR079i7tvity65TavGWzuqrGlTpAC2ZJzZSpghnjBZGMWWSsNsGe/957ZyisLjoZXdMcl2R9plIwY4ULpj/Y4xEqfPEiB7bhzC9gXz/D4A2zMiv7ZgrmZN0BztZDwews/7BXT1QwYxMNApbglzg0UTCHEuHPdgkkSzAj8h82zxheVQKXpmAOoHD8SzIFM8Z16rSpUQPWYLYO14XfYDsJs9CIYnowKBR4pgpmBATqe0tfHZgmdNbdDkuv5EmFYN63b5+CmQ/2+Dzy6COWM/DwF4880RJWe3r26qFn9jHzbCYKZpOEtz8pmF06fokI5g8//FAvz8ETglWiYLaiwmN2CCRDMBuuw7RYho11cKJgDqbh7PdkCGYIYAiF8hXKqSpVKyuY3URKH330kZ6hw30Qb8pUwRwvL6+VS6ZghhkLNpdi78dtRoCXSMFdcP8uXLjQNi7MSAdHMqVgto3O1RkpmF06PPEKZjx0sAkBMw7hEgVzODI8Ho1AooIZDw7MLFuFmKVgjkY/fecTFcx79+5VLa5poQoUzK8gYu2YBWAWunOXzgl1koI5IXyuL5wMwYyVifkL5usV2EaNGirs84mUMAMNTyKJmL9RMEci7J1zFMwuHat4BDN27RYrXlS7jYvULQrmSHR4LhKBRAQzlighlrE50SpRMFtRceZYooJ55qyZ2stALB5PYJMME4tEEgVzIvTcXzZRwQxxjM15pcuUUitXrsyy4TRc7++dea9q3KRxuNO2jlMw28Lk+kwUzC4dolgFM2Z0IJYnTpwQtUcUzFERMUMYAvEKZswoQywbEa/C1KzoJSMsmfSfSFQwx9riQ4cOaa8O8fiMDr4WBXMwDf99T1QwP/XUU2rSpInq1KlTtuHUrl1LzZk7x3Z+q4wUzFZUvHeMgtmlYxaLYP7kk08U/LCOHz/O1hszBbNLB90DzYpHMMNWGWL5+eefi9hDzjBHxJPWk+kWzBC6EEOJJgrmRAm6u3yigjnW3mETH7yPwMNLIomCORF67ilLweyescjSknbXtlMPPfxQlmNWP8A2EI7+sYsXm2zspFQL5ipVq9hpBvN4kECsghleMCCW4RUjWqJgjkYofefTLZgRvASBTBJNFMyJEnR3+XQL5kcfe1RdfXXNhKFQMCeM0BUVUDC7YhhOb8RFF1fSdlZw8h8tIey1XbGMulIlmD///HPVsFED7T4qWpt53psEYhHMa9f+R4tl+Fu2kyiY7VBKT55KF1WM6tUiWS355ptvdDjvZARg+ZcRdOK6Du2T1TTW4zIC6RbM2Lhq5Zo1ViwUzLESc2d+CmZ3jos6duyYnjWGyxs4+090SSi4m8kWzLAHgzkI2oroSNhVzORPAquNmWJ4PrATcht2y3hQ2E2pFMzYfAa/5IuXLLbbnIzOh0hnV9eqqbCRONUJYYXr1Kmd8GUQpAMTDQg+weRPAk2aNlHz5s1LS+fgdg5BYGDymGjC383Lql+WaDUs7zABCmaHByDa5eHLEZGD8uTNrSZPmaxj2kcrE+18sgQzZrURKhQmIdh5vH7D+miX5nmPE/j0009V5SqX6AiSWEIPF8I4nm6mQjDDZMkMdVv98urqwIED8TQt48rgJXjSPZNU/gL51PDhwxTEQ6pS6zatFbxqxJvg7mvAwP46nDHqwX3E5E8CZcqWVmXLllH/+c/bKe/g0qVLVbVLqyZ8HUQyRbuxz4jJ2wQomD0yfm+//Zb+5S1broxavXpVTCYYoV1MhmCGGUj9+vW0cJo3f15ShVNoe/mzuwjgRWnFihVJf1FKtmDGgwrivkLF8to7RyxmS+4i7lxrDh8+rFeNLihaRPuuTeYLEnoFrxg5zj0nrlk8vAw9OOdBHaHt5t43qaNHjzoHildOC4FffvlFmxTmzpNL3dDxBgUzwFSlTp07qQkTxsddPSYXsHkfezimz5ielMmuuBvDgkkhQMGcFIzpqeSvv/5Scx+aq847v6DC0hTCX8eTEhHMWNru1/8WdW7OHGrYsKG2lubjaSPLuJ8AZiHxQDFNcSCuEknJEszBDyrYH/7++++JNItlDQLr1q/Tq0hXXnWFgh17shL8LletFvsmYUQNRLlata5W27ZvS1ZzWI9HCOBvTdduXfTfHpgDxuImzk4Xf/31Vy103333XTvZs+T56aef1OjRo3R4bITJPnLkSJbz/MG7BCiYPTh2sG8eNGignpmJFtLTqnvxCObgpe3mLZorhN9mIgEQOHjwoOrYqaPCrA+W8TELFE9KVDCHPqiSsYksnn74tQxml2GGA1vwZO2rwCwePPzYTTCpua7Ddap4iWIKPnX/+9//2i3KfD4kADNAmAPCLBDmgclaRcL+i3Lly8ZUH+5F3JO4N2vWrKG2bN3iQ+KZ3SUKZg+PP6IWIbRnocLnq4cfeVhhBtpOilUwm0vb5SuU05u4kvVHyU5bmcc7BOAV49LLqml7PXjGiPU+iVcw80GV3nvk+++/V0OHDtGbPxPZV4FZPOzN2LlrZ9QO/Pzzz2rs2Lu0TTVm7/ByxEQCIIAXOZgFFi5SSJsJwlww0dT3lj7qjjtut13N9h3bFQKcFC12gVq0aBFf5GyT81ZGCmZvjddprYUoQYhPhPq8rPqlCqIlWrIrmIOXtqdNn8bNNNHA8rx+aXvk0Uf0S1zjxo3Unj17bFOJRzDzQWUbb9IzfvDBB6pZ82Z6Jg5+tmN9QUKodMwMRiqHc08//bQqeWEJBd/0+/fvT3o/WKE/CMBzD8wEYS4Is8FYwrIHE8DEE1ZRNm3eFHzY8jvs5mE/j2uOHHmHtsm3zMiDviBAweyLYVR6GRzL4VgWx/I4lsnDpWiCGbM3Y8aMpg1WOIA8HpXA8ePH1eDBt+kHya23DtJuEqMVikUw80EVjWZ6zkPQIoIjVp9i3VcBoTFkyOCwDcXMc926dbSbOATAYSIBOwRgLgizQbhGhIccmBPGkmDmAbOKSOY+2BcBjyz58udV8PJCV6qxEPZuXgpm746dZcvNXe3YiIUNWVabIcIJZvyBWLx4sXZ/U6PmVWrzls2W1+BBErBLABtTIaTOL3Se3rAayWzIjmDmg8ou+fTmw9hNnTZVm2ngRQlmG5ESRAxMyeD9JzQhkAmWxLG5OR7BE1off848AniRe/HFF7SHHHjKgVmh3TRixHC9R8gqP+qFfTMC+yAa5po1r1hl4zGfEqBg9unAmrvaseS5fPnyLMueVoJ5x84dtMHy6b3gdLfwkMGSPVwiwq+plUhCGyMJ5uAHFYJT8EHl9KhaX//LL79U3XvcqO1JYZoT7gUJ9wBeooJn//744w81+77ZWignsqRu3TIezUQC+JsCl25w7QYXbzAzjJTwdwab/eCFJTTt3btXtWrdStvR4z7F/cqUWQQomH083uaudmyGaNiwgUIkLKRgwfz111+r3n1upg2Wj+8Dt3QNm7ywSQxmQwjGE+pDNZxg5oPKLSNovx2w/7yqxpV6X8W6dWtPKwjvPjfd3CtwHC9AmLGrV6+u2rV7V+A4v5BAMgjAtRtcvOXMda42Nwy3aRRu5LCyEfwiB1/h2AAIO+U+fXsrPDOZMpMABXMGjLu5qx2/8IiIhV3mvXr1VLNmz9Jvy7TByoCbwEVdDPahOm7c3QGzoVDBzAeViwYtjqbghX3hwoXacwDcxx06dEjXAtMvbOKD7TPCDrdp20ZdWKqkgk9mzPAxkUCqCMDVG1y+IeoezA9D7ZQnTpyget3UU18e58z7F6HbsQrLlNkEKJgzaPzNXe14y8YsH5a2X3nl3xlEgF11E4ENGzeoK668PCCWMAN91tln6hkcPqjcNFKJtcV88UGYbeyrwIwz/v4g5DaOpSLwRGItZmk/E4AQhus3uICDKzh42jFT9csv065TsX8H+3ggrOGlJVRYm/n5mVkEsqG7wpQxBDDcw4YPFWOZW/798iuSPXv2jOk7O+o+AsaDSBY9sUiMmWapUL6CGFHbpGrVqmIE55Hp02ZIt27d5IwzznBfw9mimAkYngTk9jtulw0b1gvGvXXrNjLz3plSpkyZmOtiARJIlMDJkydl6tQp8tDDD0nXrl2l3y39pWmzJtK2bVt58cUXZfiw4TJ69BjJnTt3opdieZ8QoGD2yUCyGyTgZQInTpzQotkIQCCDBw+RSRMnSZ48ebzcJbbdggBe2I09E1KieAmZPHmKRQ4eIoH0EjDMgvSLnLERVQyTIP0iN2vmLClXrlx6G8KruZ4ABbPrh4gNJIHMIYAHFmeUM2e82VMScAsBrHJJtmwy+Z7JbmkS2+EyAhTMLhsQNocESIAESIAESIAESMBdBCiY3TUebA0JkAAJkAAJkAAJkIDLCFAwu2xA2BwSIAESIAESIAESIAF3EaBgdtd4sDUkQAIkQAIkQAIkQAIuI0DB7LIBYXNIgARIgARIgARIgATcRYCC2V3jwdaQAAmQAAmQAAmQAAm4jAAFs8sGhM0hARIgARIgARIgARJwFwEKZneNB1tDAiRAAiRAAiRAAiTgMgIUzC4bEDaHBEiABEiABEiABEjAXQQomN01HmwNCZAACZAACZAACZCAywhQMLtsQNgcEiABEiABEiABEiABdxGgYHbXeLA1JEACJEACJEACJEACLiNAweyyAWFzSIAESIAESIAESIAE3EWAgtld48HWkAAJkAAJkAAJkAAJuIwABbPLBoTNIQESIAESIAESIAEScBcBCmZ3jQdbQwIkQAIkQAIkQAIk4DIC/w+dKRTPOwbcTQAAAABJRU5ErkJggg== />"
Question 8Draw the two enantiomers of -pinene (Figure E16.1) and assign the stereocenter(s) for each isomer as R or S.
Question 9Are the ligands (DHQ)2PHAL and (DHQD)2PHAL enantiomers? Explain.