« previous next »

Author Question: What does the limit of the derivative of a function tell you? (Read 1322 times)

aero

  • Hero Member
  • *****
  • Posts: 512
on: Jun 19, 2013
Starting with the function F(x) = (x^2 - 8)/(x+3), I took the derivative of it and got (x^2+6x+8)/(x+3)^2. Then I found the limit of that as x approached infinity, and it was 1. What does that answer tell me about F(x), the original function?

And please don't post any silly answers. Thanks.


j_sun

  • Sr. Member
  • ****
  • Posts: 384
Reply #1 on: Jun 19, 2013
You did the derivative and the limit correctly.
In the limit, the slope of F is 1 means that eventually, the function F  is increasing 1 unit for every unit of x.
So the graph of F will eventual look like   F approximately =  1*x +b


Related Topics

Need homework help now?

Ask unlimited questions for free

Ask a Question
« previous next »
 

Did you know?

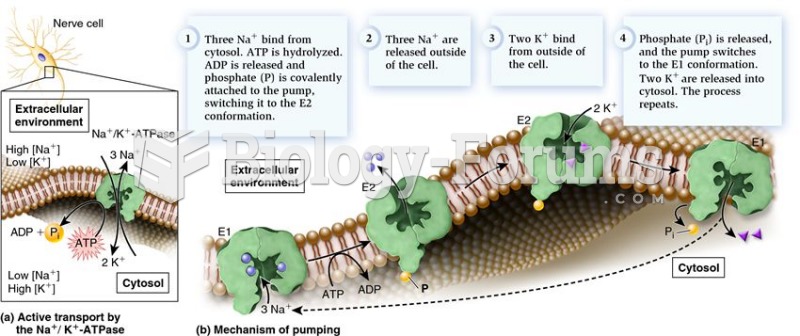
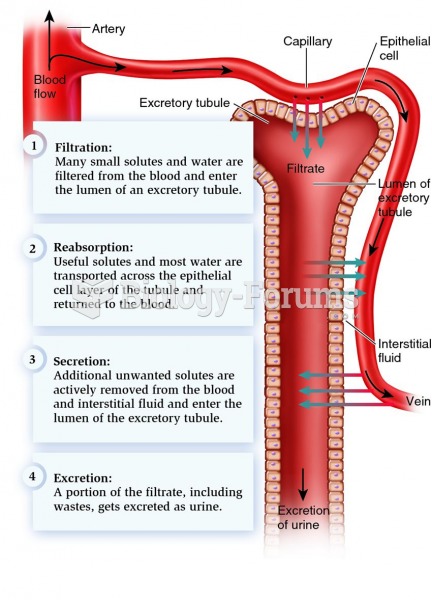
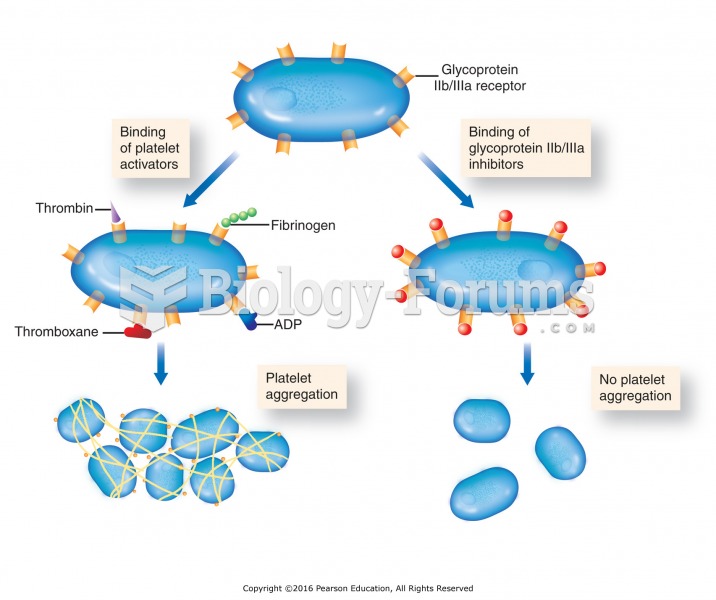
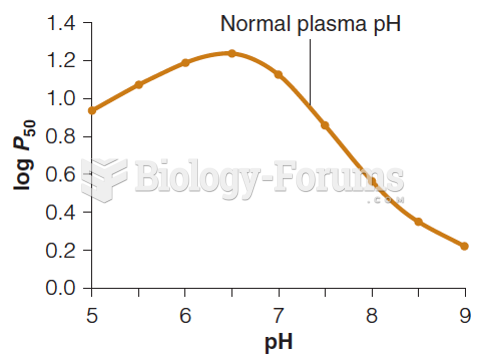
There are immediate benefits of chiropractic adjustments that are visible via magnetic resonance imaging (MRI). It shows that spinal manipulation therapy is effective in decreasing pain and increasing the gaps between the vertebrae, reducing pressure that leads to pain.

Did you know?

More than 4.4billion prescriptions were dispensed within the United States in 2016.

Did you know?

In 1835 it was discovered that a disease of silkworms known as muscardine could be transferred from one silkworm to another, and was caused by a fungus.

Did you know?

Though Candida and Aspergillus species are the most common fungal pathogens causing invasive fungal disease in the immunocompromised, infections due to previously uncommon hyaline and dematiaceous filamentous fungi are occurring more often today. Rare fungal infections, once accurately diagnosed, may require surgical debridement, immunotherapy, and newer antifungals used singly or in combination with older antifungals, on a case-by-case basis.

Did you know?

When blood is deoxygenated and flowing back to the heart through the veins, it is dark reddish-blue in color. Blood in the arteries that is oxygenated and flowing out to the body is bright red. Whereas arterial blood comes out in spurts, venous blood flows.

Structure and function of the Na+/K+ pump. Structure and function of the Na+/K+ pump.
Basic features of the function of many excretory systems. Basic features of the function of many excretory systems.
Glycoprotein IIb/IIIa receptor activation of platelet function. Glycoprotein IIb/IIIa receptor activation of platelet function.
How to find the domain and range of a function (Part 1) How to find the domain and range of a function (Part 1)
Oxygen affinity of hemoglobin as a function of pH Oxygen affinity of hemoglobin as a function of pH
Use the power rule to find derivative Use the power rule to find derivative
Video: Autonomic Nervous System Animation

For a complete list of videos, visit our video library