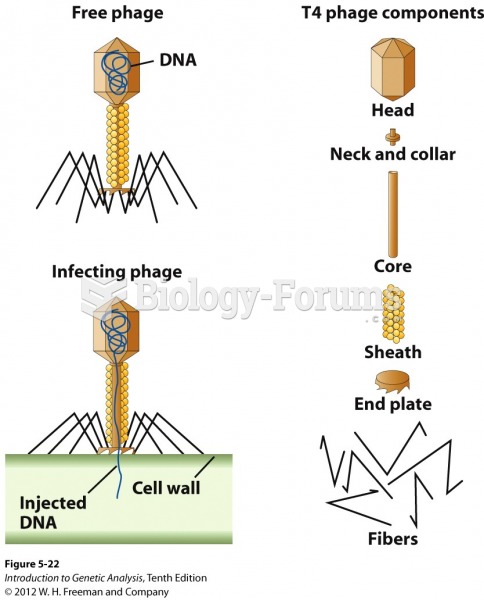
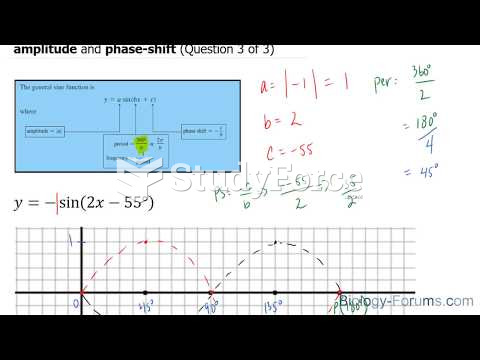
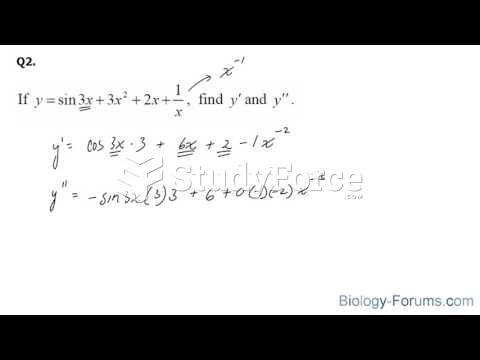« previous next »

Author Question: What does the limit of the derivative of a function tell you? (Read 1326 times)

aero

  • Hero Member
  • *****
  • Posts: 512
on: Jun 19, 2013
Starting with the function F(x) = (x^2 - 8)/(x+3), I took the derivative of it and got (x^2+6x+8)/(x+3)^2. Then I found the limit of that as x approached infinity, and it was 1. What does that answer tell me about F(x), the original function?

And please don't post any silly answers. Thanks.


j_sun

  • Sr. Member
  • ****
  • Posts: 384
Reply #1 on: Jun 19, 2013
You did the derivative and the limit correctly.
In the limit, the slope of F is 1 means that eventually, the function F  is increasing 1 unit for every unit of x.
So the graph of F will eventual look like   F approximately =  1*x +b


Related Topics

Need homework help now?

Ask unlimited questions for free

Ask a Question
« previous next »
 

Did you know?

The first war in which wide-scale use of anesthetics occurred was the Civil War, and 80% of all wounds were in the extremities.

Did you know?

Women are two-thirds more likely than men to develop irritable bowel syndrome. This may be attributable to hormonal changes related to their menstrual cycles.

Did you know?

Inotropic therapy does not have a role in the treatment of most heart failure patients. These drugs can make patients feel and function better but usually do not lengthen the predicted length of their lives.

Did you know?

Aspirin is the most widely used drug in the world. It has even been recognized as such by the Guinness Book of World Records.

Did you know?

Asthma attacks and symptoms usually get started by specific triggers (such as viruses, allergies, gases, and air particles). You should talk to your doctor about these triggers and find ways to avoid or get rid of them.

Structure and function of phage T4 Structure and function of phage T4
How to plot a sine function with a negative amplitude and phase shift (Question 3 of 3) How to plot a sine function with a negative amplitude and phase shift (Question 3 of 3)
How to find the second derivative of a function How to find the second derivative of a function
How to evaluate and sketch a piecewise function pertaining to tax (Part 3) How to evaluate and sketch a piecewise function pertaining to tax (Part 3)
The permissible exposure limit (PEL) and immediately dangerous to life and health (IDLH) ... The permissible exposure limit (PEL) and immediately dangerous to life and health (IDLH) ...
Given the parent function f(x)=log10(bottom exponent)x, state the equation of the function that Given the parent function f(x)=log10(bottom exponent)x, state the equation of the function that
Video: Osmosis - water transport

For a complete list of videos, visit our video library