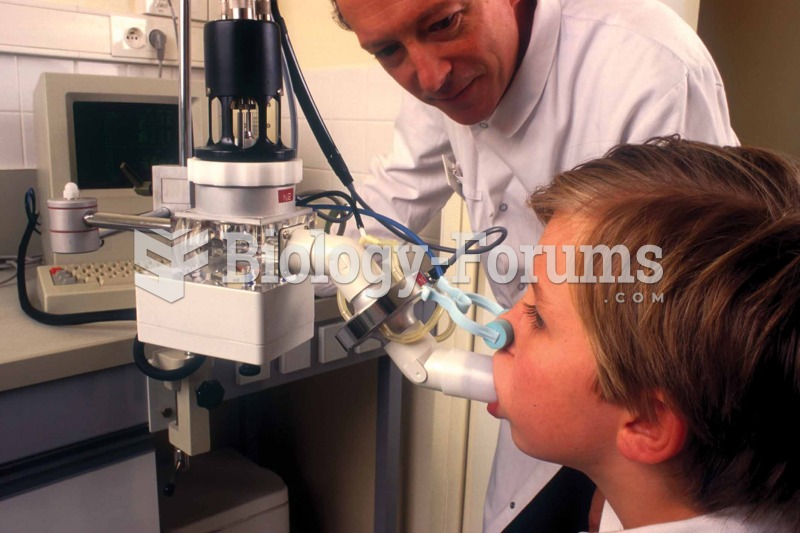
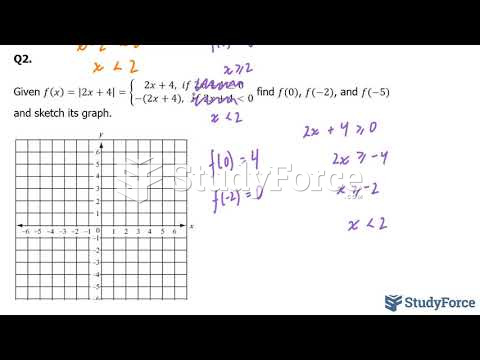
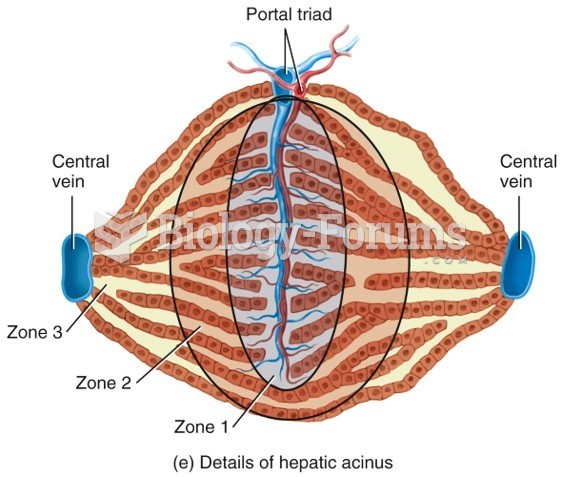
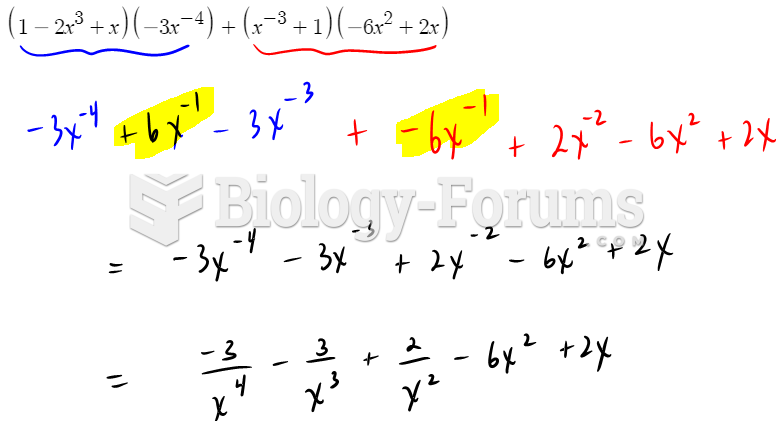« previous next »

Author Question: What does the limit of the derivative of a function tell you? (Read 1324 times)

aero

  • Hero Member
  • *****
  • Posts: 512
on: Jun 19, 2013
Starting with the function F(x) = (x^2 - 8)/(x+3), I took the derivative of it and got (x^2+6x+8)/(x+3)^2. Then I found the limit of that as x approached infinity, and it was 1. What does that answer tell me about F(x), the original function?

And please don't post any silly answers. Thanks.


j_sun

  • Sr. Member
  • ****
  • Posts: 384
Reply #1 on: Jun 19, 2013
You did the derivative and the limit correctly.
In the limit, the slope of F is 1 means that eventually, the function F  is increasing 1 unit for every unit of x.
So the graph of F will eventual look like   F approximately =  1*x +b


Related Topics

Need homework help now?

Ask unlimited questions for free

Ask a Question
« previous next »
 

Did you know?

Parkinson's disease is both chronic and progressive. This means that it persists over a long period of time and that its symptoms grow worse over time.

Did you know?

Street names for barbiturates include reds, red devils, yellow jackets, blue heavens, Christmas trees, and rainbows. They are commonly referred to as downers.

Did you know?

HIV testing reach is still limited. An estimated 40% of people with HIV (more than 14 million) remain undiagnosed and do not know their infection status.

Did you know?

Stroke kills people from all ethnic backgrounds, but the people at highest risk for fatal strokes are: black men, black women, Asian men, white men, and white women.

Did you know?

Calcitonin is a naturally occurring hormone. In women who are at least 5 years beyond menopause, it slows bone loss and increases spinal bone density.

Pulmonary function test Pulmonary function test
How to use the chain rule to find the derivative of a function How to use the chain rule to find the derivative of a function
How to evaluate and sketch a piecewise function containing absolutes (Part 2) How to evaluate and sketch a piecewise function containing absolutes (Part 2)
Hepatic Acinus Model of Liver Function Hepatic Acinus Model of Liver Function
Evaluate the Limit Question 2 Evaluate the Limit Question 2
Find the derivative using the product rule Find the derivative using the product rule
Video: Carbohydrate digestion (brush border enzymes, end products) & Carb absorption (fructose, galactose)

For a complete list of videos, visit our video library