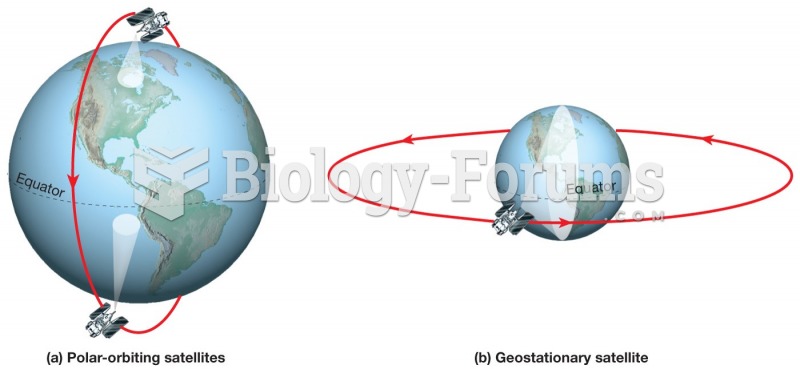
- Grade 11 and 12 Mathematics (Moderator: geoffrey)
|
|
|
- Grade 11 and 12 Mathematics (Moderator: geoffrey)
In Eastern Europe and Russia, interferon is administered intranasally in varied doses for the common cold and influenza. It is claimed that this treatment can lower the risk of infection by as much as 60–70%.
Inotropic therapy does not have a role in the treatment of most heart failure patients. These drugs can make patients feel and function better but usually do not lengthen the predicted length of their lives.
Between 1999 and 2012, American adults with high total cholesterol decreased from 18.3% to 12.9%
As the western states of America were settled, pioneers often had to drink rancid water from ponds and other sources. This often resulted in chronic diarrhea, causing many cases of dehydration and death that could have been avoided if clean water had been available.
Immunoglobulin injections may give short-term protection against, or reduce severity of certain diseases. They help people who have an inherited problem making their own antibodies, or those who are having certain types of cancer treatments.