Draw alternative chair conformations for each substituted cyclohexane and state which chair is more stable.



 Question 2
Question 26k7I8AhBZGPmKYBUUAtkTkacnIkA8O3AiQoZ7Eg00akxnmQPDAQMIqMVkhBIoIYoGVIbCxw376/vvvMwgaaLZQGsyNxAyyaAPsido+OBn2M4S/FZyL4dwoSSKQExDYu3cv93uD3125cuVSOP7r036se0ZgDwTpUNP8+fPpq6++Uh8yi304hsO5GT67cIKGryPWCmPNNhy6ESvA3AmLPBBAxt3dnfsHa+NXCkNtqMhjEoEsRODVq1c86gocmZ88ecLvhJUiK1asyLCAzUJ2c0zV1jmmpbKhEgEzQODhw4d8RQdC3WG5HAirJaAVmnNEdDOALstZkMIwyyGWN5AIvEEAw0uE1cdadCwjwxJHLN1cu3YtYS2xJNMiIIWhafGXd88hCCxbtowHDHB1dSUE+ICtDcFysVYfW0mmR0AKQ9P3geQgGyOAgAKIztyjRw9q1aqVEqkdTcawGMckmQcCBo10bR5NklxIBMwDAczCIqIKoq6MHz+eR2fPcRnnzKMrdOJCCkOdYJKFJAL6IRAcHMxTrmK2eOPGjdSuXTv9KpCljY6AHCYbHXJ5w+yOwKZNmxRfNiQwk4LQMnpcCkPL6CfJpQUggAxuEyZM4C4zCPyLiZJKlSpZAOeSRSAgh8nyOZAIGAABRFnGJAlmh5FZburUqXqnqjQAG7KKTCAghWEmwJOXSgSAANJ2YigM/8ElS5ZwoSiRsTwEpDC0vD6THJsRAkji1LlzZ7K3t+e5STKTH8WMmpUjWZE2wxzZ7bLRmUUAwZNnzZrFE5d5eXnxxGBSEGYWVdNeL4WhafGXd7dABOLj48nf358GDRrEI7cggxzS2UqybASkMLTs/pPcmwCB48eP89SZM2fOpEWLFmUqNawJ2Je3TAUBvUN4IScxImwsXryY4uLieBJ1JGX29vbmt8Dxixcv8vzJyHUKevDgAQUGBvLlR9jqk7c1Fb7lYYmAyRCACw3yZtvZ2ZmMB3ljwyOglzB89uwZ1ahRg8+eqVlB5nokkkdIIiRlx5dz+PDhNGXKFF4MAWCrV6/O9xHLLTNJ1tX3lfsSAYmARMBQCOg1TEZmemSpz5s3L23dupWw5Ehof927d6eoqKhUtT5cI9dlGqrbZD0SAYmAoRHQ2bUGwwI4lGJo8PPPP5Ofnx/nZd26dVSwYEHC0GHHjh2G5k/WJxGQCEgEjIKAzsLw0qVLXLND2CGhDYJDBwcH8vHx4T5WyJMgCPtwOQDBhohQRpIkAhIBiYC5IqCzMHz+/DkXhrD5aboRFC9enLcPIYsEXb58mbsfiP8QojKsuUAjp2+TKOriVtpyLpKSiMjO4wPq2LIMOSiwJFHE2c207VI0P5+rSGPq3KIk5VbOm3YnOeoSbd16liKSHMizeQdqWCQXZ0g5npyXvFu1o9qFdH69VA1KpqhLW2nr2QhKdvSi5h3fJw8dq4m9sppmrntNrb/pRlWc9bKAqe6fg3d1Tet3/PhxljdvXmZnZ8eioqJSXObn58dzkX700UdK/lc3Nzc2aNAg/mvevDnPsYw0g8jPKkkiwBKfsr+GlHqT0zZPc7b8fuJbUOIusYn/sX1zrtpkdjHGiOknE8LYxp/msUuxb9l5dy+K7evlzoicWfvtqnch6Qnb2AHJ091Z78Mx716m65GofayXOzFy+YTtitb1ohh2sFchRpSPdd6p4knXy2U5pvPno0qVKgRn01y5ctGxY8eUzwc88TF7DFuir6+vcrxnz540Y8YM/ps8ebJctK4gI3c4Ajb5qWyNuuRX24UobjdNW3GdXv8LTczZjXTXpwqPIuJUqhIVd9L5Mc0cuMnP6FTAx/T53HMUnZxWVfbkWuitHquUtM5Drq72yt8M79i7krbq067PiepOWEPLlqyjwEbmn7oz7baY5qyOCjiRo6Mj9yk8fPgwD2MOO6GbmxsFBAQQfA/hO4jF6phkkSQR0A0BR6rRvw9dPzWFgo8a21IAAAbsSURBVGb9Ruf6zaC6eR7Tgc2M/Oq60OJ5b2tJfvE3LRs7iQ7Ze5LDncdUdkAA9fe+Rb+PGE8bbjtTo971KXTmQrpedQL9+Wtb8qAoOr1gHM0PLUAFn72g8gP/Sz0qO5MiVuNv0eoxo2lPrkpU9NkVuu/1LY0uMYM6jTtJMTaRFDg0kGwCvianbYG07JYjOT0+Sefi69CgiUOpqbLYJJ7CtvyXuk45RNcdP6QRc0ZR4bcsv9lLSocPiqWQFeMp4K9kKvjyCoVX+Y5+HpjvzbUslv6Z9wVNXH6BbGoPoDkze5O3fQxdWv4uT03sz9Jv30+lrfdc6HFpe3JcPkU7LjaaDMr/CgL6aMchISHMycmJD18w5HV2dub7NjY2bNiwYbyqevXq8WPDhw9Xqr5w4QIfXiOjvRwmK7Dk8J0kdu+P3mziyRA2v4EdI3JhnTY9Ya9uLGYDp19k99c1YXZEzKn9NhaV+Iht+KQAI7ee7MDzOBY01pNRnkbstxvP3uwTsffa/5eNbVOcFawfyIJfJbKwpS2ZI1VgPwXHsMuTKjK7koPZiRdvIY/a0ZG52DdkC28nsoSbi1nfH06wF7Gn2dASxMi9N8MoN+HmTPYfKztWb85NFnv9F1aFiBX2P8RiWBw7P6o0I7JjDRbeZnG35rH37YjZ1gpgf/QsrBomp8dHEnuy7XNWmIqzISejWMhkb0bkw+ZfPcNGlSZGVt5sxJ7LbLu/ByNyZZ/te54GTy/Y8QHv/VvuUSq4vG2/3HsXAeVDqUjHNHbKly/Ph8RNmzblrjQxMTFUuHBhmj17No/fhkvhXA2NsVixYkpNmHEuWrQolSlTRvoaKqjIHY6AbTHqOKw9uVA0bZ62ivasO0812lakFIPNiIM0e0MEUcGy5J7bnty93Iji/qLfNt8hK2srTMFQxc8G0Y9b7lD40e+oYu5IOrFkH8Vy7XAizT0WQQm399CBO/EK6LaO+Sn3q8PUu3JN6rHGg0aOrEOOytk3O7ZFmtF3P4yiXtVj6fS+8xRBRFFhEcpwnsieChbJR/Ye9alpaaLEMxvon1fQBQSlx8dT2j99FT2mIlSthAuV/epP2n9wOXUt+q/65uRFDX3KkGe5AkT0kiJfJFJaPL3B4s29teMi+JJbbQjoJQxRQeXKlWnPnj2EWWXMMD969IjnfxWVQzAi78OAAQPEIe5ig5hvN27ckEuYFFTkzhsErKhAk2/pyxJECUeH0fDgJtSyZErrTXL8c3qeQETWNnyYa21nQxCBcdFx/4JoTTbqJzk5gV7E4oICVK/vBJq17RExFkyjK76dj3aqP4U2/dqNqrAgWjmqJfn03kGRmnZC6zyUJ+4UTeszlULcyxNEklaysScnTCizZFKLQkqPj6SXFBEJPmPoYfRrsslfiRp/4EVpTgTryhNnVAMXrczLgwIB9SMkjum0xZI6mfhaJ6hkIa0IMEpOTqIE+NY4VKc+g2uSNblS/S8bUWE8leyNWElOTCYrt1rUqhwRxT6lmMREehH+ghh5kG+TUqKYsuW3ss5HFeoUJaIQWrPtJsVTEkWe20lnI3CzNxS+61e60GQRXXhwkea2dqHwc5focSJxIUtJiZQQG0Yn/+xP3Sbvplctv6FPK+YmTVnJawKb8U8oFF5l5ZpSudwQ0/9SenzYuFFN3xJEFEz/W3aeYogoKSaM7kS/5VNUJbZRuwamz9Nb+FLiIiqRW60IZFgYaq1NHpQI6IQA/AhX0K/zNtPSwF9p47UEKtNlOHVq1IcG1HGmmODVNH3BeYLO9PL4PJq124n6L51EHyZvpwUrVtOitdFUZ/gymlAplHYevAdpREGrVtFJRdg5ks/IeTTEx4HOffcfKl+jMfXZbk8lXMTsQTIlRRyjXwYMpRmbztOjpGL00eDOVMb5PapROS9R+HLq22cRRbh50ntEdGv6p9R1chDZ5iJ6HbyJdt16TWSdj7wa1KP4nStp5W/TaKt1c5o0qyHdOB9OROF0Zvd5ikxKjw9HqjlqMY2o5URXAxqSd61W1DPgCD2+vIP+ug+F8TIdPHWB9h1CG19R8M7DFOGqnacdQWdo57FHGMhT0M5NtP4vbbjo1Dk5tpBegRpyLEqy4eaBwOtwunb5Hi
Question 3W5V6By7vZvZ4ZT5S6eIkJvUoRjafIsnLJ84rNHFJvHmWJDb9LzfJ7k5eHwpr7EZxR2+xnlLVmcXGyT6dXjULod70aexZ3p9cMb9MC6OJUunIsSoqKJ5XMl22ehdOWBNRUtV5JcUo7uVVylzgcvlPySHl69RpGOpahc8XzpJCZKjaeU7VPdXO7qiIAUhjoCJYtJBCQC2RsBOUzO3v0rWycRkAjoiIAUhjoCJYtJBCQC2RuB/wOFOdCl3SxFnAAAAABJRU5ErkJggg== />
 Question 4
Question 4Draw structural formulas for the cis and trans isomers of 1,2-dimethylcyclopropane.
Question 5Draw structural formulas for the cis and trans isomers of hydrindane. Show each ring in its most stable
conformation. Which of these isomers is the more stable?
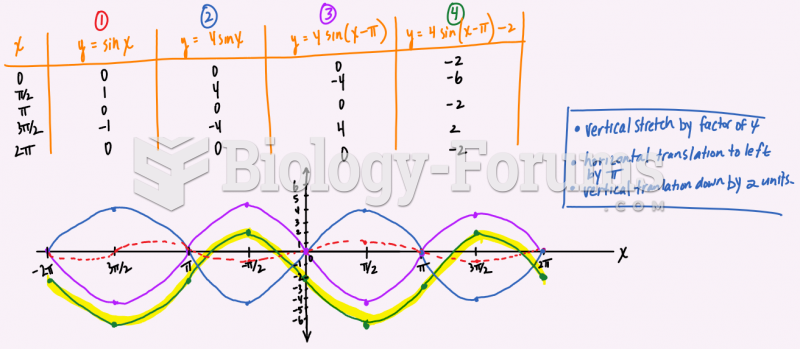
Question 67ggY2BGCWvL0009nAwcOzA+x2JZQZz35zne+kzFkWlPuuuuu3HirtRAUfW7xPYvHtZV0+ZCEpYCrvbmvmBbTIhdMNz5Z4o5pQZLzZAhbl8Gyw8ccc0y+xLGEGlMDm5KWClDcAAATYUlEQVSU155wSULidjfVsppwLVqTw721hshqlyDlzXVc/763dPpUU+tlERfvH7BwiylfvkuetDy3hEpJmkkSAgmB2giYQllvNoP9xSwmUxktEFhPHFOs2VDv2Eb369/WX6gVbqfPLU3flrOjuvQsCdnFBWEoHdQMdKT87YmNPpyedJz1DWT+ytiXr2AAsma9WSfyAjqzmJds6lM9kYNhQZzuJp6dRZqSJAQSAk1HwCwIOUbWdNGXykUugpyjJ554It8lb6jSqrPl5zFSTH1sTVFeI9d2TK38ppbWqUt7GBACXgR/XhVaCCVqW/EK2WJ7+qyMALJl6pDOYUqQBZ06O1lwJ+pdzbtUeqeOKZKWSren7wmBhEDPRWDFFVfMCbd1TUxVtEIjYTRJpLZOhjFk8cUXz7cPHDgwTzCsh5gXibW2/nRty0XXEvW2PkPxVtxaxzZ3X5cmDM296XRe90DA7IVG3sHg3RKOTZIQSAgkBEoR8Ap6a2Fcf/31+cyixRZbLH9NvfCDdVXMPChkr732yreZHVFNvD8G+dhvv/2qHdKs7WZ+CUtYcrqaXHLJJfmbK9v0raZtlRyRyk0ItDUCMoPNkLjvvvuqXspaB9ZA+Mc//lH1mLQjIZAQSAhYc8Zsu1pvmfVWWmuyvPTSS9MA9tZbb+UJktaDaQs555xzssUWW6zijDCJzxKe2/oNw106h6Ea00rbewYCwgzeJOndCUIp5keXigRAL6myQiPLIUlCICGQEKiGgDdS+qsl1nmxyqI1F+RPCWdIRHzwwQfzBHIJ45aFbwuxBovVW60BIVziTb3WXZB87SV2vK2NvPOmJXXr0q+3bsmNp3O7DwIykr1NTuxORrNZBBYzsXSqNeLrLencfZBId5IQSAi0BwKWhBbG8G4X+XIWDjQ7oilvnm1uPS0k5f0+FpHyum0v5aP3ShP/m1t2vfMSYaiHUNrfJRCYNGlS/r4HiUGSHCUJiU8WM2a6xE2kSiYEyhGY/GE8fN0dMeFbO8WGA/qU7y35PSVGvzA8bn1iZEz+79YZ5lsz1pnzxXjgpU+jeKtInwEbxnYbLRJfviKt5PTSr1NGx/PDb40nR06O3rMvG9/davXoX9EXPS5e+eO5cdPE78QBOywXs/03I27K6Odj+K1PxsjJvWP2Zb8bW63ePyqeXnrN9L1rINAWsZZUZkIgIZAQSAi0HIFJb5yVrRKRff0Xz2bTrutZVv6kD7I79l7gy/fqLH9y9syYL7JswjvZn3aYK9/We9Uzsr+P/aLspMo/v/hwWLb17JHF/PtmD42pfEw25oFsr/6Rxde2y+74ymtWvsg+HLZ1NntENv++D2XVTq9SatrciRFIxK9r8LpUy4RAQqAHIjD94nvHrc+tE5OWWD761rv/6eeKpZb1ptb3os/8g2LhWZn8c8dSA+eKiJEx26KDYsGZG5sY13umftGv3gVnXTNOvOHKWGfSurH+l0vf/LeGvWOmfv3q17fe/aT9nQ6BRBg63SNJFUoIJAR6HgJT4pMXro9zrn0h/vPhhFj58JNiiwnD4/Jbn403R80Xu/1ypZj3jT/GqWc+EdPP2yfGTlou9vn59rF4rShFJRCnjIpHzzgkTrzz/ei1wLfj4BO2j7j+pLh67NZx6i/WiQ8uGhJHXT4iZhm8Unxm7aGZI2LK6Hjy/CPjhGFvxWzr7x1r/+OsuOi1FeLwIYvHvRf8Od6b4z+x0lqHxfITn4jzhxwVl4+YJQav9FkUp0dMiTHPD43Tr3wzZpnl3Xj4iQmx1mGnxeEb9I2nzjs8TrrlnZhzve1j4IiL49rnIgbvd35ccMCyMfHxC+PY81+NOeYcE2OXPyRO2H35qWGPSreWtrU9Ao3RzbavR7pCQiAhkBDooQhMiVEPHBXrbXhWzLjNBvHZ7WfEcZeOiD4Dl40xV58WZz3YK+ac4YMYtvfucc7IDeKAvZaLd/4+IfrWMPcmPvP7+PEuu8Quu+wRR//pn//DtXe/WG3btWPsg/fFnY9+GvPNPyCW7t8nVtx2w+hz+49i4wMvi093uiyu+/mqMd3E/57We45Ybq3+8fK9d8e1510T/5l/jvh4xLPx/vyrxKzP3Rd33/lMfDThw7jlRxvHgZd9Gjtddl38fNXpojg9Jr8Vl+/5wzjtsf6x3ZFHxAbvXhk/2/W4eHTcnLH8mnPHiHvvimuuHxErHXl0rDHq0Rh67OnxyItXx84b7B/3Lrl3HPmjxeLOfbeIYx8f+7/7SN86BIEaTa5D6pMumhBICCQEehYCox+Io3Y+Pd7e4LbYc+V1YsKdj8URi60cfT++Lh54M2Kpo9aLBfv0jXkW6Bujrj4sfr3//XHG2TPGXONHxGWn/CGe/mRK9Jpx0dj2yANjwH+R6zP4kLhg6NbRLybE3094Km574dWpmE6/yHZx+JZHx8N/vCIuemyHWOWFwbH5LhPjiePvjNGxUKy79oCYud/ischsU0+J6NU7ekXEDMvsEgeftE0cf5IlER+LQ2wknz4RV9w5OmKhdWPtATNHv8UXiamnT79AbDzk+Dh63Erx+ZP3x3MjI2LU2zFyYoTl/RUxy5Lrx9oDl4yXRE9eHxUf/O3yuHdsxDxPXRqnffRqfDzprbj7L2/HhDWWqZ2w+d/qpI+2QSARhrbBtQ1KbcUs6JgSo58fHrc+OTIm9549lv3uVrF65TToGPfKH+PcmybGdw7YIZb7Xxp0g1nUbQBDKjIh0M0Q+OSxP8SN7/WNNX+wRvTrPWPESqvH/BHx8cPD4smJC8aumywRM8Yssf4pZ8X379olfrXLL2OzF86K5f/vp3HCry6JtydHzLTyL2Pvk6drDJnec8UGh+4UC/7xvBh69Kkxeb9TYvc+E+Ppj8ZFxHzRd4bqjufe01XZN+nT+PL0vjHt6b1jppk+j7+duG+8ceAJkadU/KdWVbP4YuzYmBQRc66xdxx7xNLxy9/VOj7tay8Eqjz99rp8F7/OF6PixSf/lcfq2v5Oesccg9aI/o/9IixRuteZH8Ty6y4di66yZsx+zxH5tr0v+CQGrz2gAQbeO+ZYbs2Y7bafxF57HByXvfrlGurT3sNn8cTpB8QRR+8fJz4y5n+7uSjXnC1u+8lescfBl0XV0/93RvqWEEgIVEFg8if/jjExw5cD9eR3444Lb4t/Tv4sXhz+aHw6+2qx1ud3xz3DT42zPtgizrt8t+j/9i1x80vjYo4NL463Jn35Lp1xT/08lp8xwnSIcpm6LZv6LWb9xo9jn0ERY57+MNbecOGYPmaJJVZdKE+OfP2D8RFfjI9xRuzIviyzOLf4LL/IzEvEl6e/Hl+ePi4f8MPxH98VB+98Wtw1/jtx6M7LRt9ijmd5GVN/94qZl1oj1OalG26LNyZETBn1TNz55Mj4Yuox6UtHIJAIQ3NRn/JJPHnGLrHX9e9Onffc3KIaPm9qFnT8Lwu6T5EFHU3Kgo7eM0W/+mnQseaJN8SVl/8xTv9qGnQ0lEXd8I2lAxMCPReBr33zgNh50TFx024bxMY/OC5GLLd2LDT95Bgz6vOIz/4ef35l4Vjw/dvjzKNOjzvenTEWXH372Gop2YilMiVGP3ttnHPNK/nGiU9dEmcPezHeeviKOHfYl+8++OThi+L84W99aeDMOCh2PWidGLDp/vGd+XkmZolVDj8r9h00NoYdsGPsMeTieGVixHRTXo67Hnw5nrrjgXgnIiY8e21c+5iBe0p8/Owd8cgHXCHPxf1vLBaHnbVvDBo7LA7YcY8YcvErMTGmiykv3xUPj5ojFl8wIt78Xey0wynx9HR9Iia+GDf/+dn42/D7492IGDPigfjbM/fGX11k/Evx0Pg94tyfrBozPzUkVhm4cmyw320x4yJzRIM+lFJg0vdWRCAt3NQcMMf/PX6/0/fi0JvejgW3PD7O/9nK8d79T8Qr70wf623TP+656t+x7enHxDcnPRjnnnx5vDj7N2KVGV6P/2/v/uOiru8Ajr88+XFyAw78HQoKpxMTM9TVA3NqpdWyNqeOGa5W5piPpZLhsuWjqPlQVIaMuehhZtLcYz6a4jKaqDUePHSZIioaaMbhYR1w0wMCjh933H32gJORPIYIjqXy5g8eB3y/d9/P8/PHfbjv675XYohlZXg+f9r/GReqgvn5klAObtjKmeFLSF41jf52I7vWpZDrMRgvm4Nxv3iZ6Ksy6CaKfz+JsLh8vGZlULa/9RzleCISzuM/fx+mnd+jsKMK+tVH8T2ZRvyq7RTq7mZC7XukZfsQm3OMZwt+266CvouEtGhMG9eRWarnBxveYkWEndy0b1TU76WR7RPLofNvEqVOs2Pju1zQ6TAfzqUxagWJL0zk4paOKujxaCuPseWVNM7rA6ixRbD8taeIaD3t0Z15kX1E4FYVsFspNn6Nf2go/VuvquS0Ya3uS0CAFkeFBbunizJzE0NHDce328+cLuq+PMMXmlGEFG0kxbWMhBkBbWrOWsxFFrxCgvCoc+EX6NOlJ2lnrZkiixchQR7UufwI9HEfqKvBQrGpkYGGYHztZRSVaggOHYy2k39ZG63FGK06Qg2db9s2CLnVYwI38TUibuJDs6nclSMUPrPV7n8ppZwX1ZbJKAbNVD95NFIF+E5Vf/x0l1o00ldFJuQq84fzlJ5+6qGd5UrVHFJLglDeUb9Wa9YmqbhxKIYtU0dqnarszzOUT+AClWUtVTtjfqzSze0vsuJQxpS7Wi7CwsBpan5MjIqJWaBmR2hbfuc/f5+qVEo5itPUfZ4owl5SJ+odyvh2rNpwsl45yzPUXD1KMylZnbOZ1LYH+ykYqmIP1aj6U6uVofn1x6A56tXVj6ngAVPUxgKr+uS5IAWBauFHFao8Y67So1GTks8pm2mberBf64VdHMqYOlH18Zyi3jDa1BfJ4xUMUYtzapTt+ItqJChNRLzKzP9ALRqKInCh+sh6UaU/olOMWaMKagrUmnBPNSLuiKq9iWddDk0EbnkBR5HaNAHFnXEq4YVUlW+75UckA/g/CnSyvuuxdcqtfcd2Ewc/NOE5aR73Nle9NiNHTICfgWfTc6mo+CtDkhbzdu1cEpdNoMFYzNee9/DE1IE0WfL41Axan0HMfiqc0q/Ad9L9jNJp0A68A23FX1ixwciM5D/ww8ENFL6zmuVLl7J0WTy/y2krhdwV9A527HiHdXODr/J0V9B6MDZX0IVkN1fQY7VU56bjDpmnMNwnkNBvZtBXVdB7Kbl0mPix3vTR/CeDJje9o4ragztmxZPw0jNMqD9OtjuDpsRqb1dBj3YHT3UV1FqPsL05g67OY1viWxytdGA68A9Kmt+8LV8iIAI9I+ARQnRSCi8+3J8xi55hfPszGz3zqHKvt4mALBi6MZHO0hz2nIWIufcxSAN1n/+d7EswZuESvt9fg/OrDNbvrmTYgliidMW8n36KPpHRTBsMlkMZnEHPzOeeJPj0uxyo+g7TfxZF84uC+hlrSZ03gML1C1nzuS/+NUdIfm09qZs3s3lrNg2Bftd3tK0VNKUtFfTRu2dhaD5tWH2Z5g7aU+tJRxPfYQWNg+qWDPpKnNXuSDT9+lF/NInYdZ8xwNC8irr2l8tRi82dQbP4lU3sLVOogt8wtvXl2GvvLn8VARHoloAHQx9YTmLSaqLDdd26B9mp9wp09LzRe0U6HbmLy0czyFcGZoYVsveMlQtZmZgYz9PR3215h0L9xROUqL6ERY2kJiuR5DwXox8aRUluIcd259E04HF+OV3L6V3ZVOmmMtvrKIVl/2R9ajmPv7GdJweV8P7fzlKnf4CtJkfLp6GpujxejvC+gQoadGGTW8pja1E5DThpcGfQLSGz+1tzFN1WUl9N4XONirqS/ctiSNzfwCNxMdzZeQaNxi+ce90ZNJnuDJqTWcexSgZ9Nbv8JAIiIAI3iYAsGLo8ES5sl2toopxDH9uJDLOyf/dZGLeAx64EitoRU5no5yRn+RxWnQpmhBeU5hyg0tdMxic2/KdHE+nvoMpSC/YvOWYJJcRRwAcpq9i4z4x30D1E/2h0y1VZ2w7vRito0E1cSWpsOLaMX7Hg6Xi2ujNozmVl8XFm+woaXJWn2OfOoMnPNjJyRQcV9eEK9O4Mmk1P/JS1J/rihZ2CPbvJ3PPfK+iDp4YR/+bzTPbJI37iGCLvX0Kmdwj6bsdcbVJySwREQARE4H8vIO+S6I6pq45Ll50EDPLt8GNbm6pMGKv7YwjW0VB6gSr/kQTp2q3PGisor9MxJMAbGiuw2D1xlZlpGjqK4d3OoDupoHFSay7C4hVCkEcdLr9AroTM1yfRUUXtasBSbKJxoIFgXztlRaVogkMZ3HkGTbHRii7U0Pm213eEspUIiIAIiEAPCMiCoQdQv9W7bDKSMtnA8444Eh4OZc7rSyVs+lYnRB5cBERABG4PAbk09O0xj22juFJBl++rkQq6TUVuiYAIiIAI3KCAvMJwg4CyuwiIgAiIgAj0BoF2J9V7w5BljCIgAiIgAiIgAl0VkAVDV8VkexEQAREQARHohQKyYOiFky5DFgEREAEREIGuCsiCoatisr0IiIAIiIAI9EIBWTD0wkmXIYuACIiACIhAVwVkwdBVMdleBERABERABHqhwL8BgykaqGD85D8AAAAASUVORK5CYII= />
Shown above are the trans and cis isomers of hydrindane. Note that the cis-hydrindane displays some distortion
from the ideal cyclohexane ring structure. The result is that the trans-hydrindane is the more stable.
"
Question 7Trans-1,4-di-tert-butylcyclohexane exists in a normal chair conformation. Cis-1,4-di-tert-butylcyclohexane,
however, adopts a twist-boat conformation. Draw both isomers and explain why the cis isomer is more stable in the twistboat conformation.
Question 8How many different staggered conformations are there for 2-methylpropane? How many different eclipsedconformatio ns are there?
Question 9Torsional strain resulting from eclipsed C-H bonds is approximately 4.2 kJ (1.0 kcal)/mol, and that for
eclipsed C-H and C-CH3 bonds is approximately 6.3 kJ (1.5 kcal)/mol. Given this information, sketch a graph of energy
versus dihedral angle for propane.
Question 10Write IUPAC names for these alkanes and cycloalkanes.

 Question 11
Question 11Each of the following compounds is either an aldehyde or a ketone (Section 1.3C). Which structural
formulas represent the same compound? Which represent constitutional isomers?